Home
Class 9
MATHS
If the non-parallel sides of a trapezium...

If the non-parallel sides of a trapezium are equal, then

Text Solution

Verified by Experts

Given ABCD is a trapezium whose non-parallel sides AD and BC are equal.

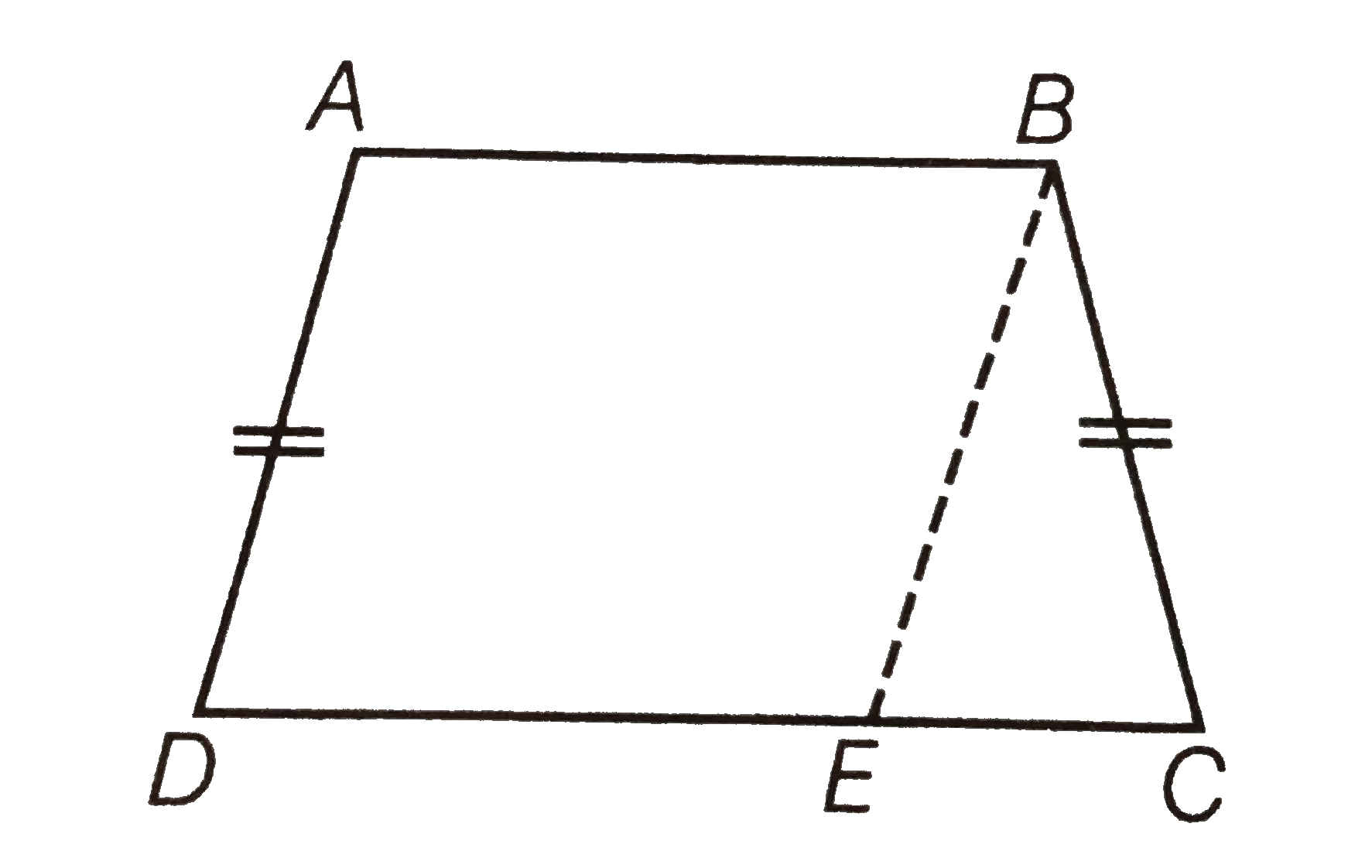
To prove Trapezium ABCD is a cyclic.
Join BE, where `BE||AD`.
Proof Since, `AB|| DE and AD||BE`
Since, the quadrilateral ABCD is a parallelogram.
`:. angleBAD=angleBED` ...(i)
[opposite angles of a parallelogram are equal]
and AD=BC ..(ii)
[opposite sides of a parallelogram are equal]
But AD=BC [given]...(iii)
From Eqs. (ii) and (iii), BC=BE
`rArr angleBEC=angleBCE` .....(iv)
[angles opposite to equal sides are equal]
Also, `angleBEC=angleBED=180^(@)` [linear pair axiom]
`:. angleBCE+angleBAD=180^(@)` [from Eqs. (i) and (iv)]
If sum of opposite angles of a quaderilateral is `180^(@)`, then quadrilateral is cyclic.
Hence, trapezium ABCD is a cyclic.
Promotional Banner

Topper's Solved these Questions

  • CIRCLES

    NCERT EXEMPLAR|Exercise Exercise 10.4|2 Videos

  • Areas of Parallelograms and Triangles

    NCERT EXEMPLAR|Exercise Areas Of Parallelograms And Triangles|34 Videos

  • CONSTRUCTIONS

    NCERT EXEMPLAR|Exercise Long Answer Type Questions|5 Videos

Similar Questions

Explore conceptually related problems

If the non-parallel sides of a trapezium are equal,prove that it is cyclic.

Consider the following statements : 1. If non-parallel sides of a trapezium are equal, then it is cyclic. 2. If the chord of a circle is equal to its radius, then the angle subtended by this chord at a point in major segment is 30^@ . Which of the above statements is/are correct?

If the non parallel sides of a trapezium are equal. Prove that it is cyclic.

If two non-parallel sides of a trapezium are equal; it is cyclic.

If two non-parallel sides of a trapezium are equal; it is cyclic.

If two non-parallel sides of a trapezium are equal,it is cyclic.OR An isosceles trapezium is always cyclic.

Prove that the segment joining the middle points of two non-parallel sides of a trapezium is parallel to the parallel sides and half of their sum.

If the parallel sides of a trapezium are 8 cm and 4 cm, M and N are the mid points of the diagonals of the trapezium, then length of MN is