Home
Class 9
MATHS
P ,\ Q\ a n d\ R are, respectively, the ...

`P ,\ Q\ a n d\ R` are, respectively, the mid points of sides `B C ,\ C A\ a n d\ A B` of a triangle `A B C`

Text Solution

Verified by Experts

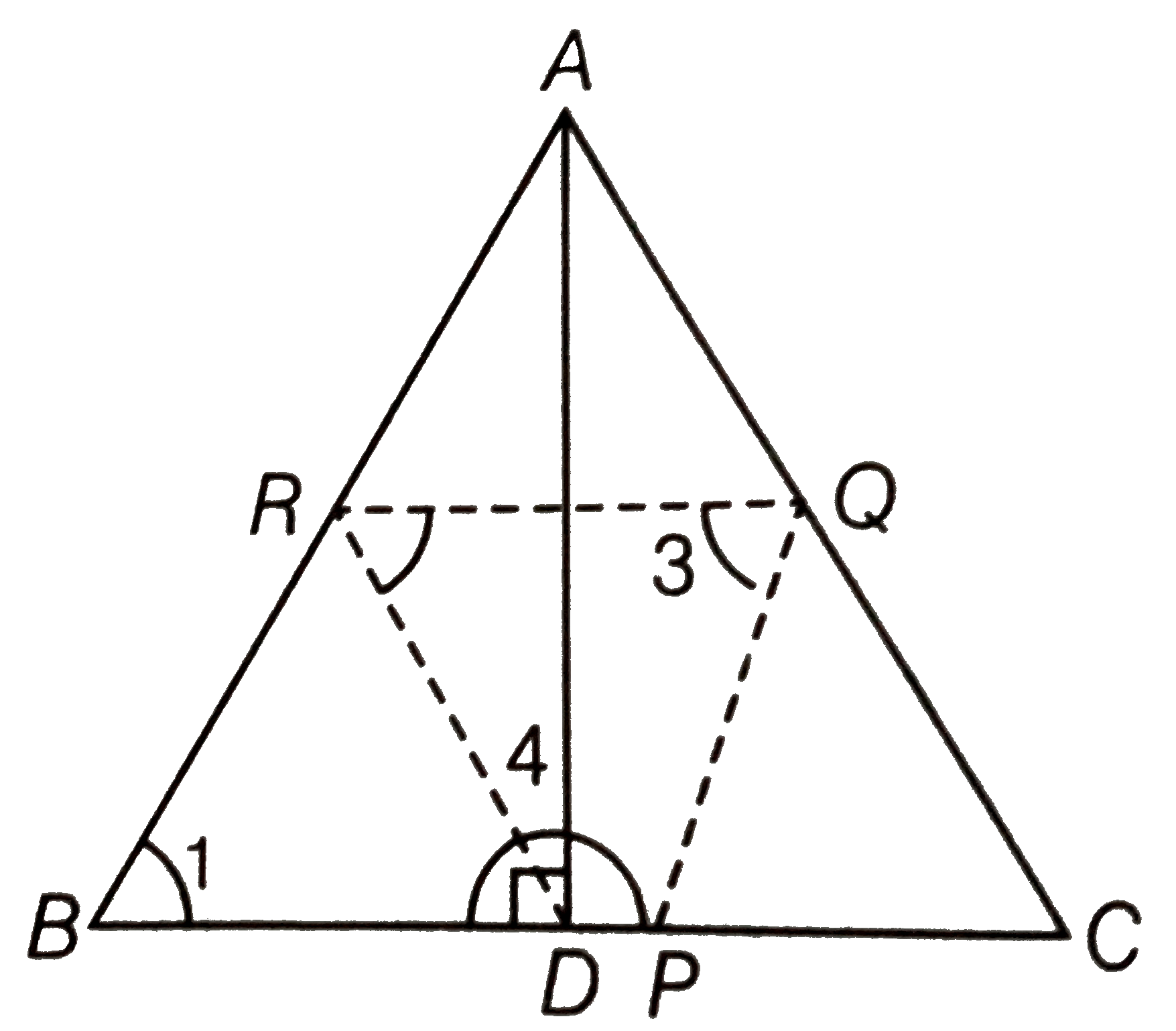
Given In `DeltaABC` , P, Q and R are the mid-points of the sides BC, CA and AB respectively Also, `AD bot BC`.
To prove P, Q, R and D are concyclic.
Construction Join DR, RQ and QP
Proof In right angled `DeltaADP` , R is the mid-point of AB.
`:. RB=RD`
`rArr angle2=angle1` ....(i)
[angles opposite to the equal sides are equal]
Since, R and Q are the mid-point of AB and AC, then
`RQ||BC` [by mid-point theorem]
or `RQ||BP`
Since,` QP||RB`then quadrilateral BPQR is a parallelogram.
`rArr angle1=angle3` ..(ii)
[opposite angles of parallelogram are equal]
from Eqs. (i) and (ii),` angle2=angle3`
But `angle2+angle4=180^(@)` [linear pair axiom]
`:. angle3+angle4=180^(@) [:'angle2=angle3]`
Hence, quadrilateral PQRD is a cyclic quadrilateral.
So, points P, Q, R and D are con-cyclic.
Promotional Banner

Topper's Solved these Questions

  • CIRCLES

    NCERT EXEMPLAR|Exercise Exercise 10.4|2 Videos

  • Areas of Parallelograms and Triangles

    NCERT EXEMPLAR|Exercise Areas Of Parallelograms And Triangles|34 Videos

  • CONSTRUCTIONS

    NCERT EXEMPLAR|Exercise Long Answer Type Questions|5 Videos

Similar Questions

Explore conceptually related problems

In A B C ,\ D ,\ E\ a n d\ F are, respectively, the mid-points of B C ,\ C A\ a n d\ A B . If the lengths of side A B ,\ B C\ a n d\ C A are 7cm, 8cm, and 9cm, respectively, find the perimeter of D E F

In Figure, B E_|_A C ,\ A D is any line from A\ to\ B C intersecting B E in HdotP ,\ Q\ a n d\ R are respectively the mid-points of A H ,\ A B\ a n d\ B Cdot Prove that /_P Q R=90^0

In a triangle, P ,\ Q\ a n d\ R are the mid-points of sides B C ,\ C A\ a n d\ A B respectively. If A C=21\ c m ,\ B C=29 c m\ a n d\ A B=30 c m , find the perimeter of the quadrilateral A R P Q

E , F , G , H are respectively, the mid-points of the sides A B ,B C ,C D and D A of parallelogram A B C D . Show that the quadrilateral E F G H is a parallelogram and that its area is half the area of the parallelogram, A B C Ddot GIVEN : A quadrilateral A B C D in which L ,F ,G ,H are respectively the mid-points of the sides A B ,B C ,C D and D Adot TO PROVE : (i) Quadrilateral E F G H is a parallelogram a r(^(gm)E F G H)=1/2a r(^(gm)A B C D) CONSTRUCTION : Join A C and H F

Given A B C , lines are drawn through A ,\ B\ a n d\ C parallel respectively to the sides B C ,\ C A\ a n d\ A B ,\ forming P Q Rdot(F igu r e) .Show that B C=1/2Q R

In A A B C ,\ P\ a n d\ Q are respectively the mid-points of A B\ a n d\ B C and R is the mid-point of A Pdot Prove that: a r\ ( P B Q)=\ a r\ (\ A R C)

In A A B C ,\ P\ a n d\ Q are respectively the mid-points of A B\ a n d\ B C and R is the mid-point of A Pdot Prove that: a r\ ( R Q C)=3/8\ a r\ (\ A B C)

In A A B C ,\ P\ a n d\ Q are respectively the mid-points of A B\ a n d\ B C and R is the mid-point of A Pdot Prove that: a r\ (\ P R Q)=1/2a r\ (\ A R C)

In Figure, A B C D is a trapezium in which A B\ D C\ a n d\ D C=40\ c m\ a n d\ A B=60\ c mdot If X\ a n d\ Y are, respectively, the mid-points of A D\ a n d\ B C , prove that: a r\ (t r a pdotD C Y X)=9/(11)\ a r\ (t r a pdot(X Y B A)

D ,\ E ,\ F are the mid-point of the sides B C ,\ C A\ a n d\ A B respectively of A B Cdot Then D E F is congruent to triangle. A B C (b) AEF (c) B F D ,\ C D E (d) A F E ,\ B F D ,\ C D E