Home
Class 9
MATHS
In the figure, AB and CD are two chords ...

In the figure, AB and CD are two chords of a circle, interacting each other at a point E. Prove that `angle AEC` = `1/2`(angle subtended by arc `CXA`. at the center + angle subtended by arc `DYB` at the center).

Text Solution

Verified by Experts

Given In a figure, two chords AB and CD intersecting each other at point E.
To prove `angleAEC=1/2`
[angle subtended by arc `C xx A` at centre + angle subtended by arc DYB at the centre]

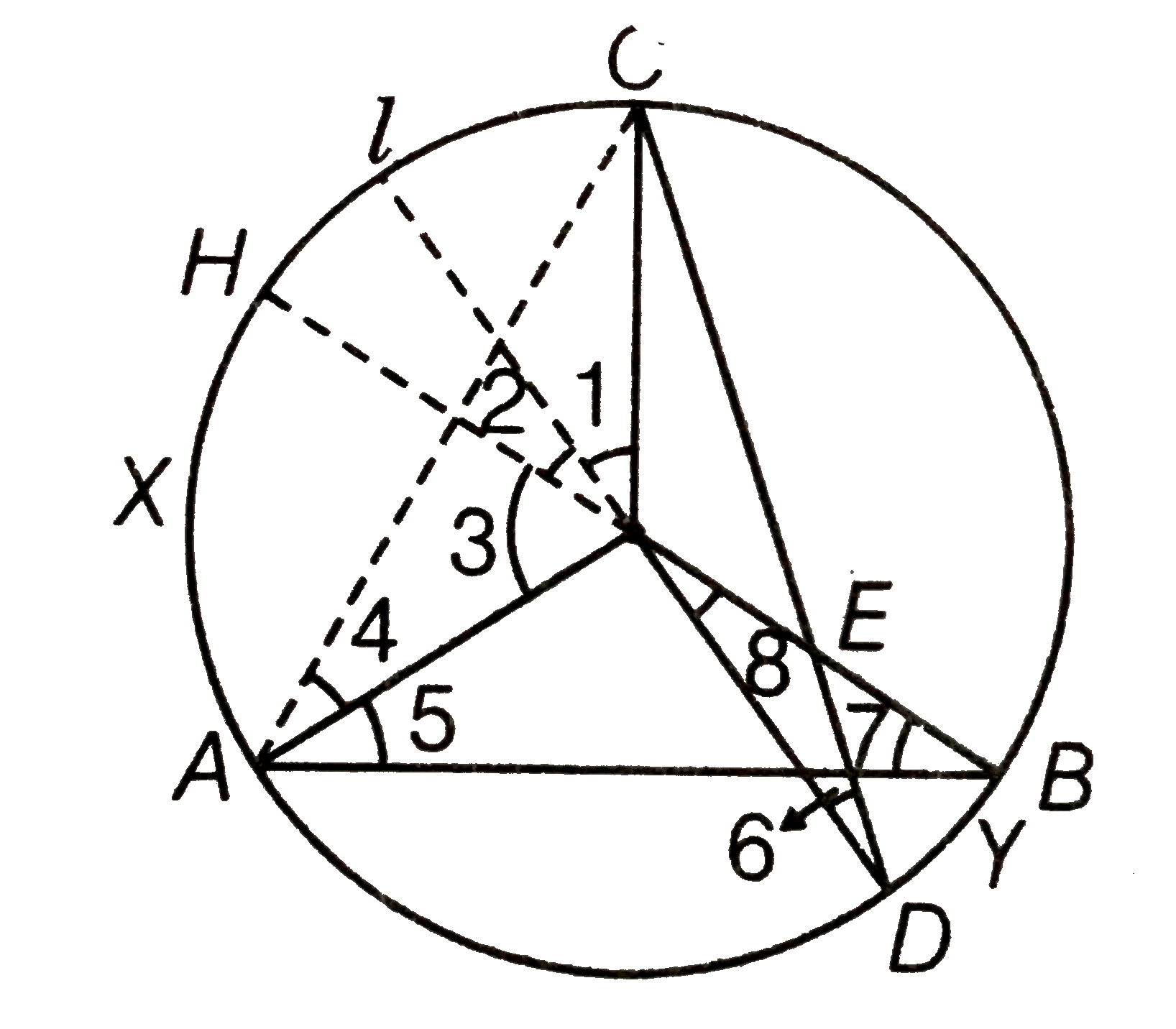
Construction Extend the line DO and BO at the points l and H on the circle. Also, join AC.
Proof We know that, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
`:. angle1=2angle6 ` ...(i)
and ` angle3 = 2 angle7` ....(ii)
In ` DeltaAOC, OC=OA ` [ both are the radius of circle]
`angleOCA=angle4` [angles opposite to equal sides arc equal]
Also, ` angleOCA+angleOCA+angle4=180^(@)`
[by angle sum property of triangle]
` rArr angleAOC+angle4+angle4=180^(@)`
`rArr angleAOC=180^(@)-2angle4` ...(iii)
Now, in `DeltaAEC, angleAEC+angleECA+ angleCAE=180^(@)`
[by angle property sum of a triangle]
`rArr angleAEC=180^(@)-(angleECA+angleCAE)`
`rArr angleAEC=180^(@)-[(angleECO+angleOCA)+angleCAO+angleOAE]`
`=180^(@)-(angle6+angle4+angle4+angle5)`
[in `DeltaOCD, angle6=angleECO` angles opposite to equal sides are equal]
`=180^(@)-(2angle4+angle5+angle6)`
`=180^(@)-(180^(@)-angleAOC+angle7+angle6)`
[from Eq. (iii) and in `DeltaAOB, angle5=angle7`, as (angles opposite to equal sides are equal)]
`angleAOC-(angle3)/2-(angle1)/2` [from Eqs. (i) and (ii)]
`=angleAOC-(angle1)/2-(angle2)/2-(angle3)/2-(angle2)/2["adding and subtracting " (angle2)/2]`
`=angleAOC-1/2(angle1+angle2+angle3)+(angle8)/2[:' angle2=angle8" (vertically opposite angles)"]`
` =angleAOC-(angleAOC)/2+(angleDOB)/2`
`rArr angleAEC=1/2(angleAOC+angleDOB)`
`1/2` [angle subtended by arc CXA at the centre + angle subtended by arc DYB at the centre]
Promotional Banner

Topper's Solved these Questions

  • CIRCLES

    NCERT EXEMPLAR|Exercise Exercise 10.4|2 Videos

  • Areas of Parallelograms and Triangles

    NCERT EXEMPLAR|Exercise Areas Of Parallelograms And Triangles|34 Videos

  • CONSTRUCTIONS

    NCERT EXEMPLAR|Exercise Long Answer Type Questions|5 Videos

Similar Questions

Explore conceptually related problems

In the figure,AB and CD are two chords of a circle,interacting each other at a point E. Prove that /_AEC=1/2 (angle subtended by arc CXA.at the centre + angle subtended by arc DYB at the centre).

In a circel with centre O. chords AB and CD interest inside the circumference at E. Prove that angle AOC+BOD=2angle AEC .

Theorem 10.8 : The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.

If the chord of a circle is equal to the radius of the circle,then the angle subtended by the chord at a point on the minor arc is:

Show that any angle in a semi-circle is a right angle. The following arc the steps involved in showing the above result. Arrange them in sequential order. A) therefore angleACB=180^(@)/2=90^(@) B) The angle subtended by an arc at the center is double of the angle subtended by the same arc at any point on the remaining part of the circle. c) Let AB be a diameter of a circle with center D and C be any point on the circle. Join AC and BC. D) therefore angleAD = 2 xx angleACB 180^(@)=2angleACB(therefore angleADB=180^(@))

Theorem 2: The no.of Radians in an angle subtended by an arc of a circle at the centre = arc/radius

The angle subtended by a minor arc in its alternate segment is…………….

Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle.Prove that /_ABC is equal to half of the difference of the angles subtended by the chords AC and DE at the center.

If the angle subtended by two chords of a circle at the centre are equal; the chords are equal.