Home
Class 9
MATHS
If bisectors of opposite angles of a cyc...

If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.

Text Solution

Verified by Experts

Given, ABCD is a cyclic quadrilateral.
DP and QB are the bisectors of ` angleD and angleB`, respectively.
To prove PQ is the diameter of a circle.
Construction Join QD and QC.

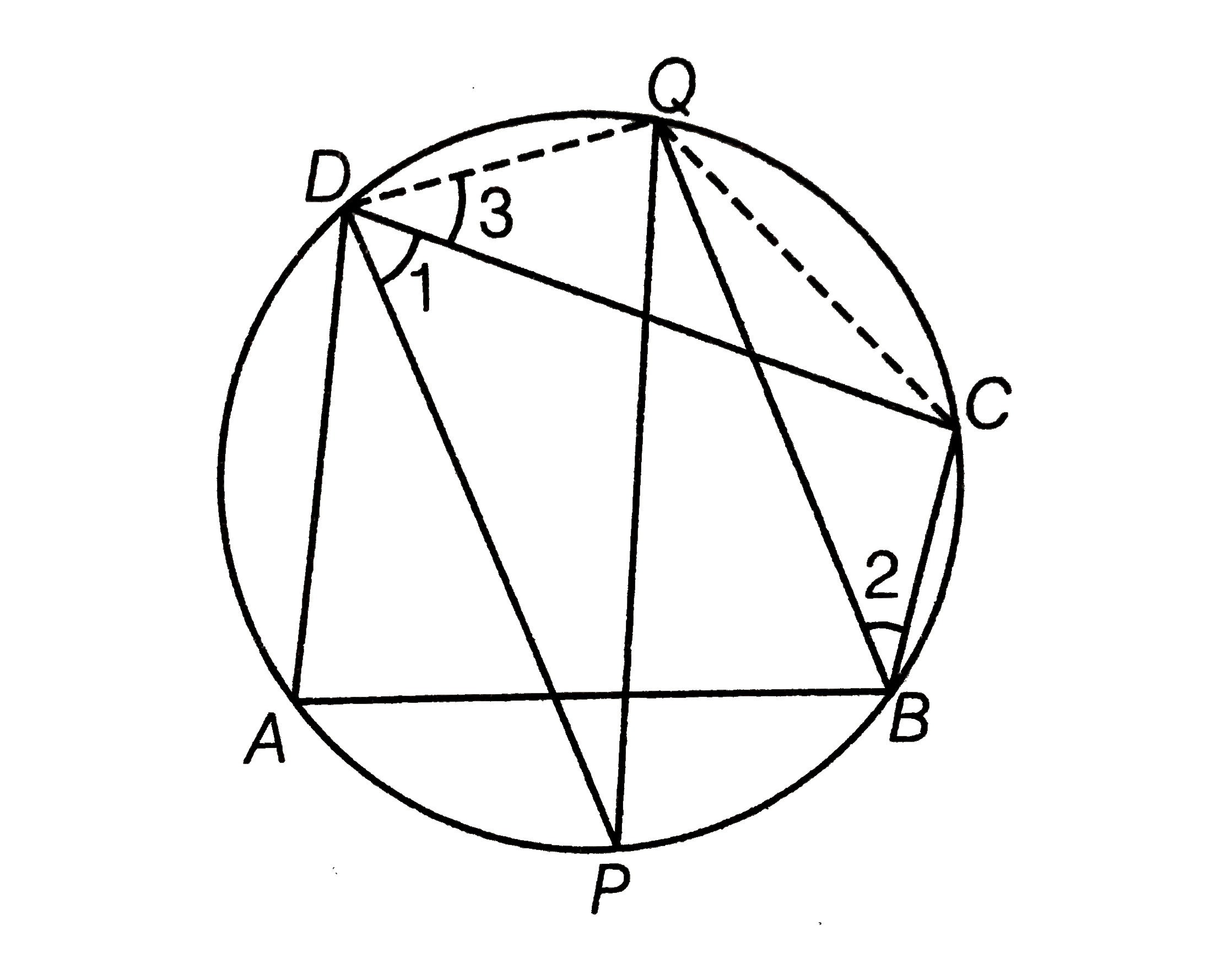
Proof Since, ABCD is a cyclic quadrilateral.
`:. angle CDA+ angleCBA = 180^(@)`
[sum of opposite angles of cyclic quadrilateral is `180^(@)`]
On dividing both sides by 2, we get
`1/2angleCDA+1/2angleCBA=1/2 xx 180^(@)=90^(@)`
`rArr angle1+angle2=90^(@)`...(i)
`[angle1=1/2angleCDA and angle2=1/2angleCBA]`
But ` angle2=angle3` [ angles in the same segment QC are equal] ...(ii)
`angle1+angle3=90^(@)`
From Eqs. (i) and (ii), `anglePDQ=90^(@)`
Hence, PQ is a diameter of a circle, because diameter of the circle.
Subtends a right angle at the circumference.
Promotional Banner

Topper's Solved these Questions

  • CIRCLES

    NCERT EXEMPLAR|Exercise Exercise 10.4|2 Videos

  • Areas of Parallelograms and Triangles

    NCERT EXEMPLAR|Exercise Areas Of Parallelograms And Triangles|34 Videos

  • CONSTRUCTIONS

    NCERT EXEMPLAR|Exercise Long Answer Type Questions|5 Videos

Similar Questions

Explore conceptually related problems

If the bisectors of the opposite angles /_P and /_R of a cyclic quadrilateral PQRS intersect the corresponding cicle at A and B respectively,then AB is a diameter of the circle.

If the bisectors of the opposite angle /_P and /_Rof a Cyclic quadrilateral PQRS intersect the cooresponding circle at A and B respectively; then AB is a diameter of the circle.

The diagonals AC and BD of a cyclic quadrilateral ABCD intersect each other at the point P. Then,it is always true that

If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral,prove that it is a rectangle

If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral,prove that it is a rectangle.

Point O is the centre of a circle . Line a and line b are parallel tangents to the circle at P and Q. Prove that segment PQ is a diameter of the circle.

ABCD is a cyclic quadrilateral such that AB is the diameter of the circle circumscribing it and angleADC = 145^(@) . What is the measure of angle(BAC) ?

ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and angle ADC= 146^@.angleBAC is equal to: