Home
Class 9
MATHS
A circle has radius sqrt2cm it is divide...

A circle has radius `sqrt2`cm it is divided into 2 segments by a chord of length 2cm prove that angle subtended by the chord at a point in major segment is `45^@`

Text Solution

Verified by Experts

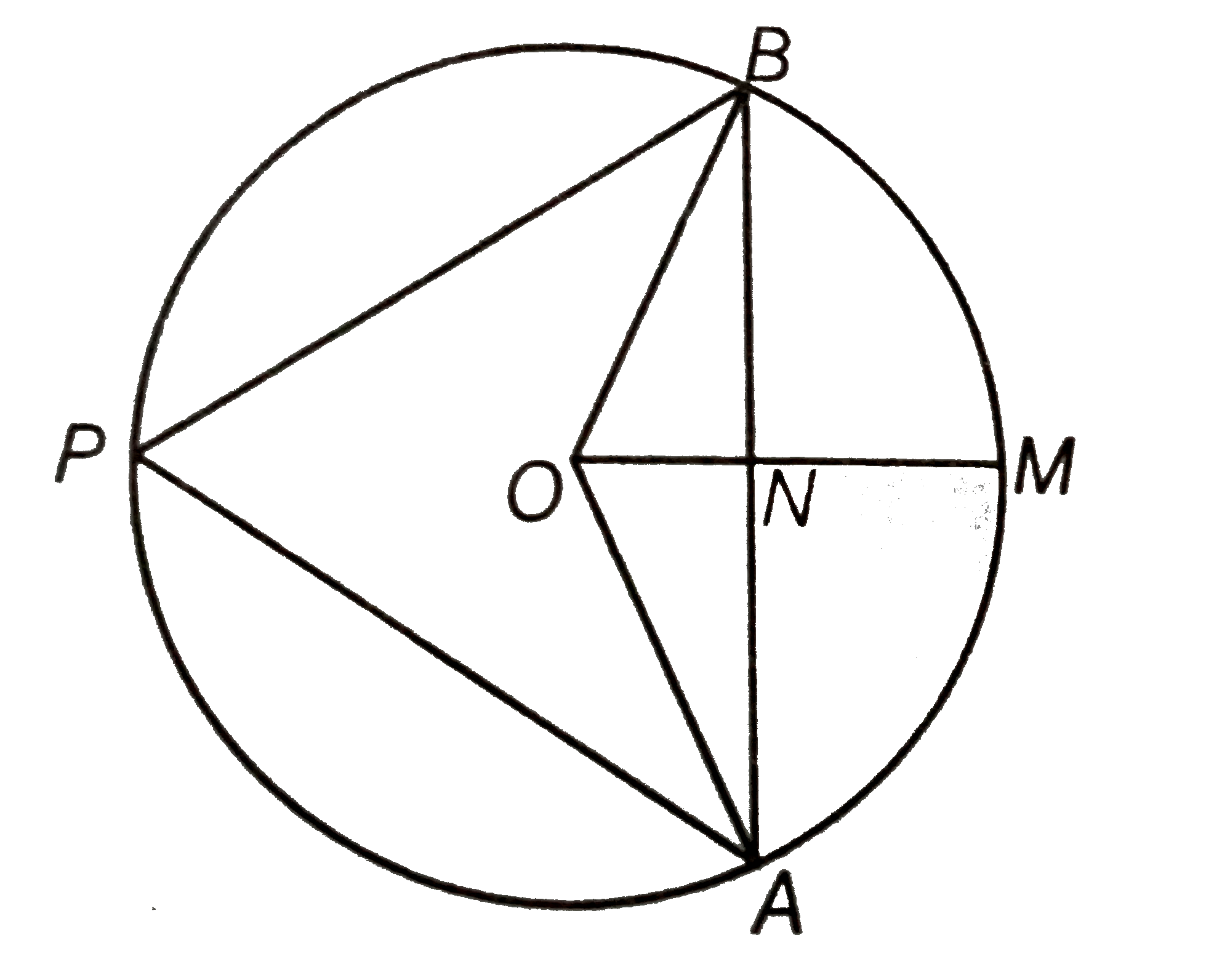
Draw a circle having centre O. Let AB=2 cm be a chord of a circle. A chord AB is divided by the line OM in two equal segments.
To prove ` angleAPB=45^(@)`
Here, AN=NB = 1 cm
and ` OB=sqrt2 c m `
In `DeltaONB, OB^(2)=ON^(2)+NB^(2)`
[use Pythagoras theorem]
`rArr (sqrt2)^(2)=ON^(2)+(1)^(2)`
` rArr ON^(2)=2-1=1`
`rArr ON=1 cm`
[taking positive square root, because distance is always positive]
Also, `angleONB=90^(@)` [ON is the perpendicular bisector of the chord AB]
`:. angleNOB=angleNBO=45^(@)`
Similarly, `angleAON=45^(@)`
Now, ` angleAOB=angleAON+angleNOB`
`=45^(@)+45^(@)=90^(@)`
We know that, chord subtends an angle to the circle is half the angle subtended by it to the centre.
`:. angleAPB=1/2 angleAOB`
` =90^(@)/2=45^(@)`
Promotional Banner

Topper's Solved these Questions

  • CIRCLES

    NCERT EXEMPLAR|Exercise Exercise 10.4|2 Videos

  • Areas of Parallelograms and Triangles

    NCERT EXEMPLAR|Exercise Areas Of Parallelograms And Triangles|34 Videos

  • CONSTRUCTIONS

    NCERT EXEMPLAR|Exercise Long Answer Type Questions|5 Videos

Similar Questions

Explore conceptually related problems

A circle has radius sqrt(2)cm it is divided into 2 segments by a chord of length 2cm prove that angle subtended by the chord at a point in major segment is 45^(@)

Consider the following statements : 1. If non-parallel sides of a trapezium are equal, then it is cyclic. 2. If the chord of a circle is equal to its radius, then the angle subtended by this chord at a point in major segment is 30^@ . Which of the above statements is/are correct?

If the chord of a circle is equal to the radius of the circle,then the angle subtended by the chord at a point on the minor arc is:

A chord of a circle is equal to its radius. The angle subtended by this chord at a point on the circumference is

A chord of a circle is equal to the radius of the circle.Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc

A chord of a circle is equal to the radius of the circle.Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.

A chord of a circle is equal to the radius of the circle find the angle subtended by the chord at a point on the monor arc and also at a point on the major arc.

Draw a chord of length 6 cm in a circle of radius 4 cm and shade the major segment.

x-y+b=0 is a chord of the circle x^2 + y^2 = a^2 subtending an angle 60^0 in the major segment of the circle. Statement 1 : b/a = +- sqrt(2) . Statement 2 : The angle subtended by a chord of a circle at the centre is twice the angle subtended by it at any point on the circumference. (A) Both 1 and 2 are true and 2 is the correct explanation of 1 (B) Both 1 and 2 are true and 2 is not a correct explanation of 1 (C) 1 is true but 2 is false (D) 1 is false but 2 is true