`AB and CD` are equal chords of a circle whose centre is O, when produced these chords meet at E,Prove that `EB=ED`.

Explanation

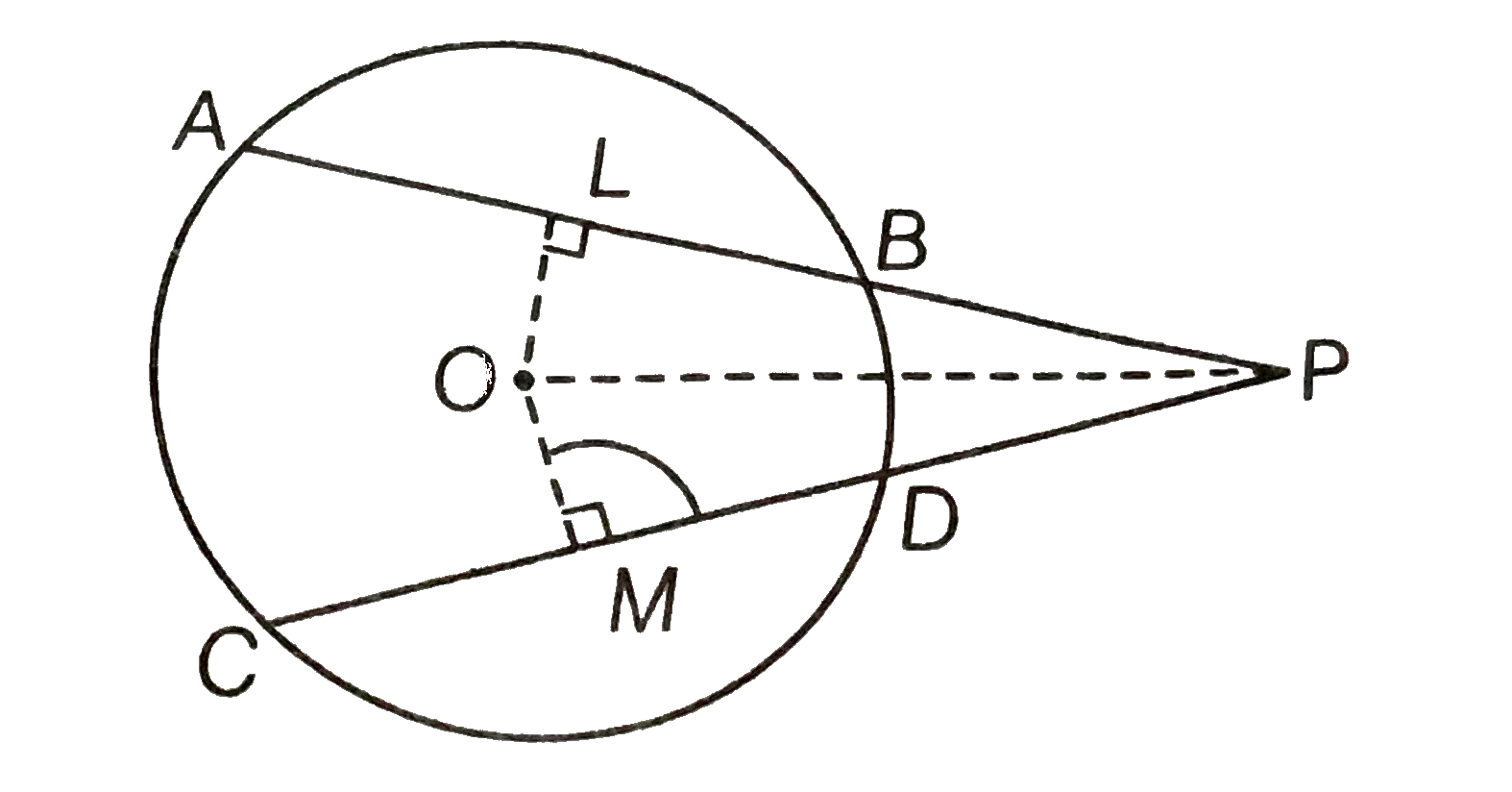
Given Two equal chords AB and CD of a circle intersecting at a point P.
To prove PB=PD
Construction Join OP, draw `OL bot AB and OM bot CD`
Proof We have, AB=CD
`rArr OL = OM `
[equal chords are equidistant from the centre]
In ` Delta OLP and DeltaOMP, OL=OM` [proved above]
` angleOLP=angleOMP ["each "90^(@)]`
and OP=OP [common side]
`:. DeltaOLP cong DeltaOMP` [by RHS congruence rule]
`rArr LP=MP` [by CPCT] ...(i)
Now, AB=CD
`rArr 1/2(AB)=1/2(CD)` [dividing both sides by 2]
`rArr BL=DM` ..(ii)
[perpendicular drawn from centre to the circle bisects the chord i.e., AL = LB and CM =MD]
On subtracting Eq. (ii) fromEq. (i), we get
` LP-BL=MP-DM rArr PB=PD`