Given In a circle of radius r, there are two chords AB and AC such that AB= 2AC. Also, the distance of AB and AC from the centre are p and q, respectively.
To prove ` 4q^(2)=p^(2)+3r^(2)`,
Proof Let AC=a, then AB = 2a
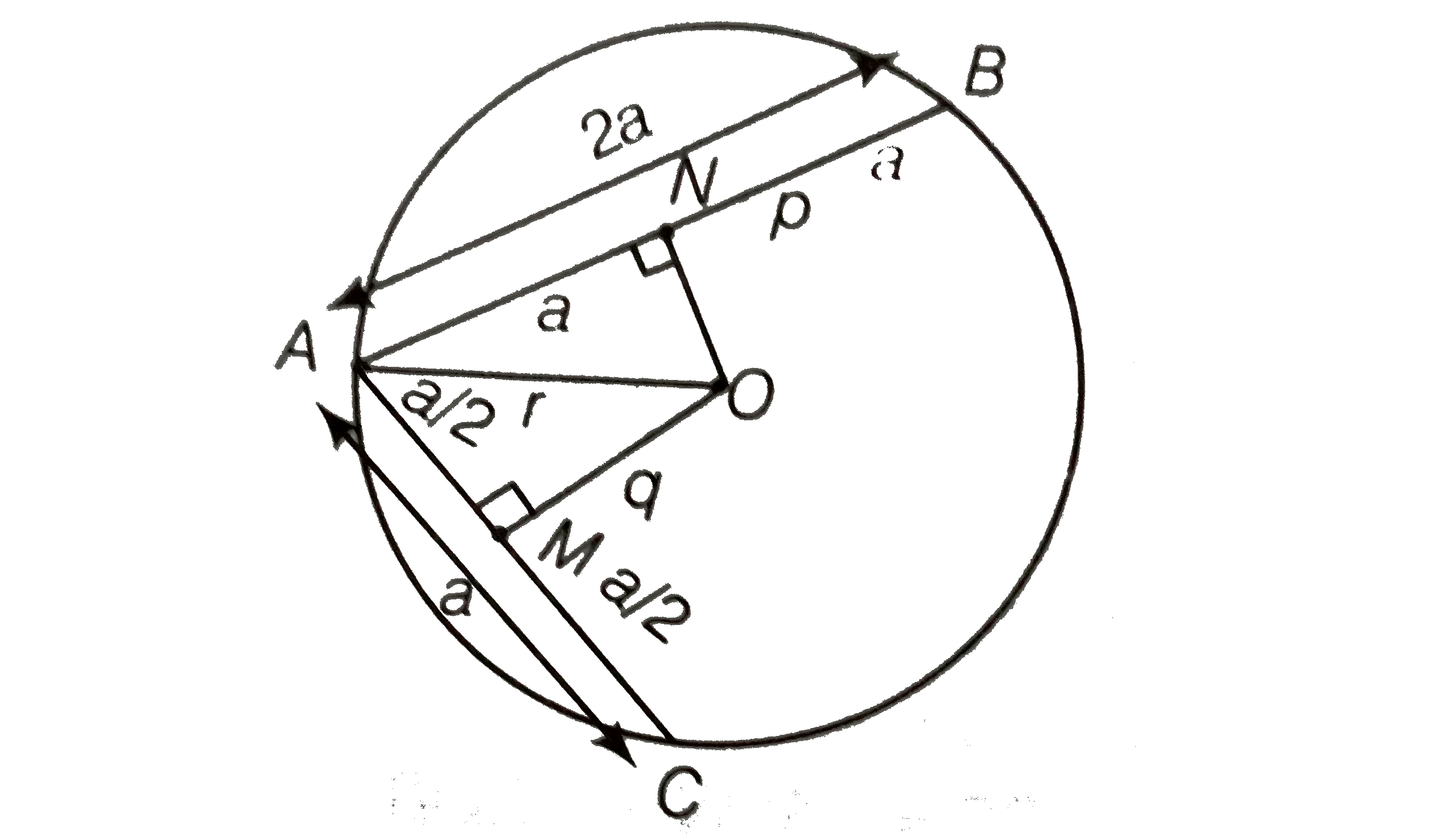
From centre O, perpendicular is drawn to the chords AC and AB at M and N, respectively.
`:. AM=MC=a/2`
AN=NB=a
In ` DeltaOAM AO^(2)=AM^(2)+MO^(2)` [by Pythagoras theorem]
`rArr AO^(2)=(a/2)^(2)+q^(2)` ....(i)
In ` DeltaOAN`, use Pythagoras theorem,
`AO^(2)=(AN)^(2)+(NO)^(2)`
`rArr AO^(2)=(a)^(2)+p^(2)` ...(ii)
From Eqs. (i) and (ii),
`(a/2)^(2)+q^(2)=a^(2)+p^(2)`
`rArr a^(2)/4+q^(2)=a^(2)+p^(2)`
`rArr a^(2)+4q^(2_)=4a^(2)+4p^(2)` [multiplying both sides by 4]
`rArr 4q^(2)=3a^(2)+4p^(2)`
`rArr 4q^(2)=p^(2)+3(a^(2)+p^(2))`
`rArr 4q^(2)=p^(2)+3r^(2) ["In right angled "DeltaOAN,r^(2)=a^(2)+p^(2)]`