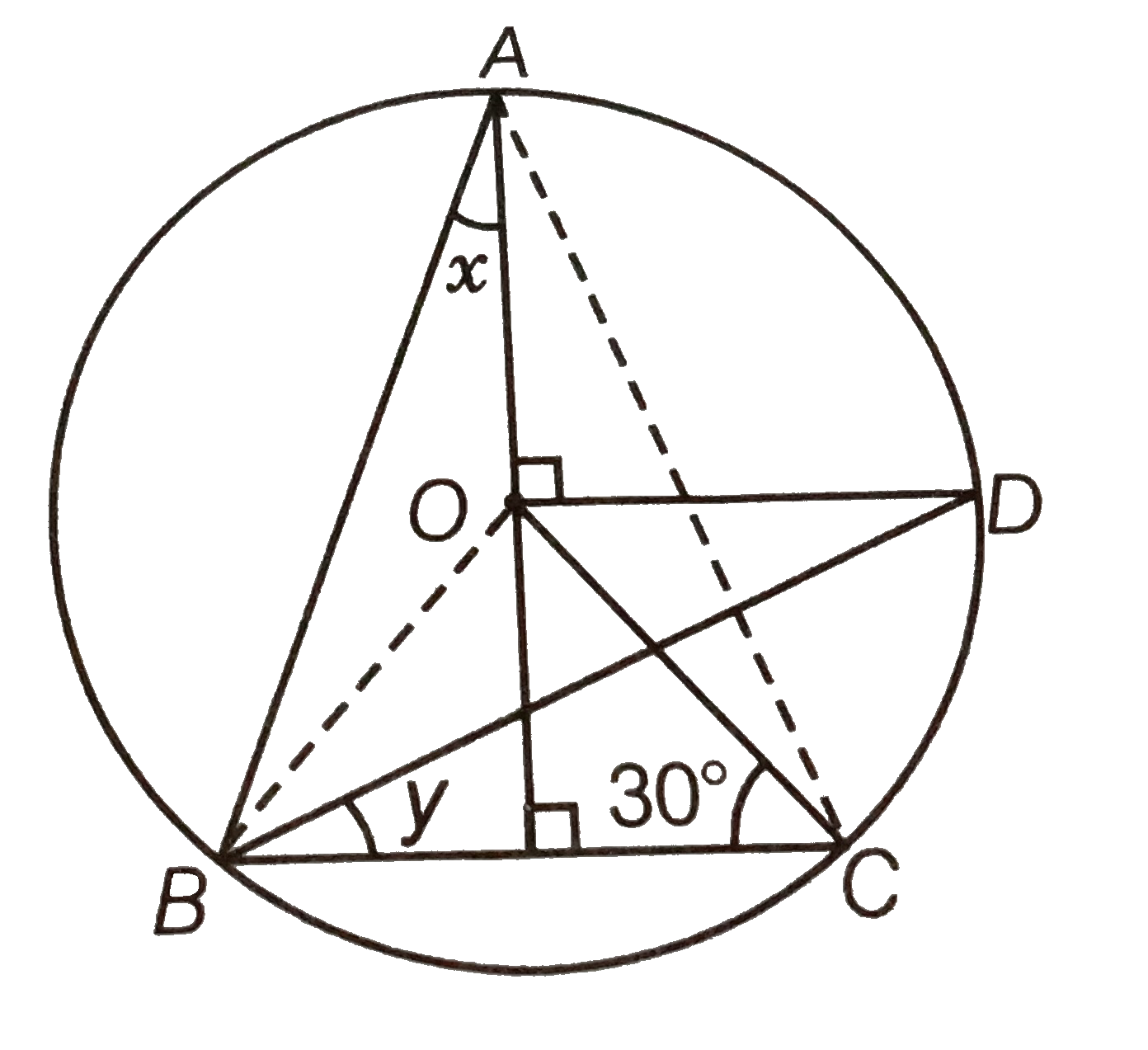Given, O is the centre of the circle and `angleBCO=30^(@)`. In the given figure join OB and AC.
In ` DeltaBOC`,
CO=BO [both are the radius of circle]
`:. angleOBC=angleOCB=30^(@)`
[angles opposite to equal sides are equal]
`:. angleBOC=180^(@)-(angleOBC+angleOCE)`
[ by angle sum property of a triangle]
`=180^(@)-(30^(@)+30^(@))=120^(@)`
`angleBOC=2angleBAC`
We know that, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
`:. angleBAC=(120^(@))/2=60^(@)`
Also, ` angleBAE=angleCAE=30^(@)` [[AE is an angle bisector of angle A]
`rArr angleBAE=x=30^(@)`
In ` Delta ABE, angleBAE+angleEBA+ anlgleAEB=180^(@)`
[by angle sum property of a triangle]
`rArr 30^(@)+angleEBA+90^(@)=180^(@)`
`:. angleEBA=180^(@)-(90^(@)+30^(@))=180^(@)-120^(@)=60^(@)`
Now, `angleEBA=60^(@)`
` rArr angleABD+y=60^(@)`
`rArr 1/2 xx angleAOD+y=60^(@)`
[in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle]
`rArr (90^(@))/2+y=60^(@) [:' angleAOD=90^(@)," given"]`
`rArr 45^(@)+y=60^(@)`
`rArr y=60^(@)-45^(@)`
`:. y=15^(@)`