Given, in the figure` BD=OD, CD bot AB`.
In ` Delta OBD, BD=OD` [given]
OD=OB [both are the radius of circle]
`:. OB=OD=BD`
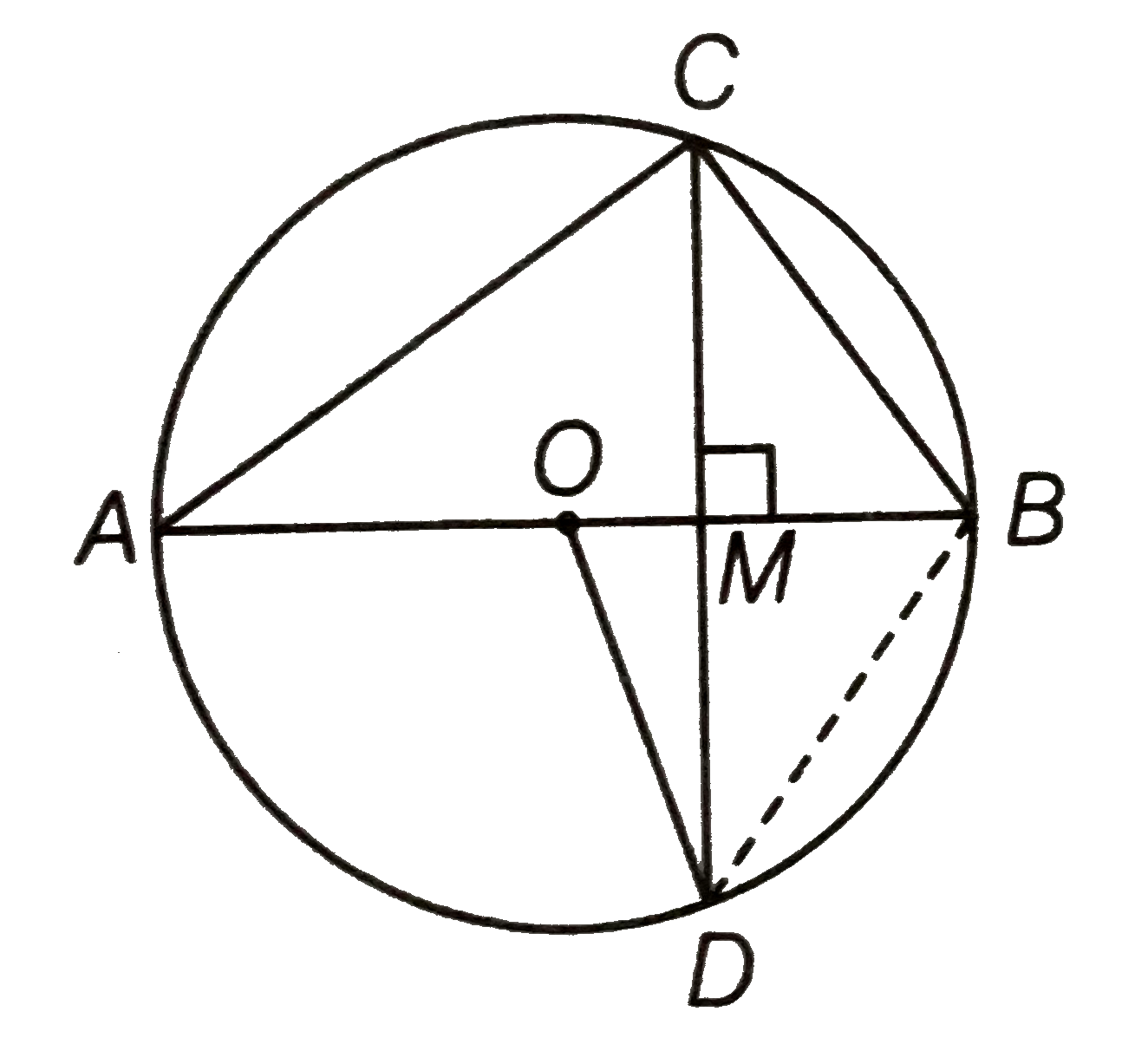
Thus, `DeltaODB` is an equilateral triangle.
`:. angleBOD=angleOBD=angleODB=60^(@)`
In ` DeltaMBC and DeltaMBD, MB=MB` [common side]
` angleCMB=angleBMD=90^(@)`
and CM=MD
[ in a circle, any perpendicular drawn on a chord also bisects the chord]
`:. DeltaMBC cong DeltaMBD` [by SAS congruence rule]
`:. angleMBC=angleMBD` [by CPCT]
`rArr angleMBC=angleOBD=60^(@) [:. angleOBD=60^(@)]`
since, AB is a diameter of the circle.
` :. angleACB=90^(@)`
In ` DeltaACB, angleCAB+angleCBA+angleACB=180^(@)`
by angle sum property of a triangle]
`rArr angle CAB+60^(@)+90^(@)=180^(@)`
`rArr angleCAB=180^(@)-(60^(@)+90^(@))=30^(@)`