Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MOTION-NEWTON'S LAWS OF MOTION & FRICTION -Exercise - 3 Section-B
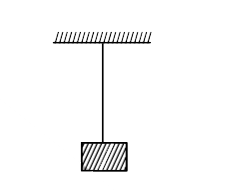
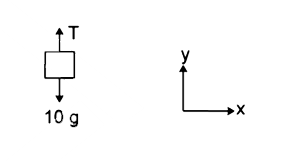
- A 'block' of mass 10 kg is suspended with string as shown in figure. F...
Text Solution
|
- The upper half of an inclined plane with inclination phi is perfectly ...
Text Solution
|
- A smooth block is released at rest on a 45^(@) incline and then slides...
Text Solution
|
- A partical of mass 0.3 kg is subjected to a force F = - kx , Where = ...
Text Solution
|
- Consider a car moving on a straight road with a speed of 100m//s. The ...
Text Solution
|
- A block is kept on a frictionless inclined surface with angle of incli...
Text Solution
|
- A block of mass m is connected to another block of mass M by a spring ...
Text Solution
|
- Two fixed frictionless inclined plane making angles 30^(@) and 60^(@) ...
Text Solution
|
- The minimum force required to start pushing a body up a rough (frictio...
Text Solution
|
- A block of mass 'm' is placed on a rough surface with a vertical cross...
Text Solution
|
- Given in figure are two blocks A and B of weight 20N and 100N, respect...
Text Solution
|
- A point particle of mass m, moves long the uniformly rough track PQR a...
Text Solution
|
- Two moasses m(1)=5kg and m(2)=10kg, connected by an inextensible strin...
Text Solution
|