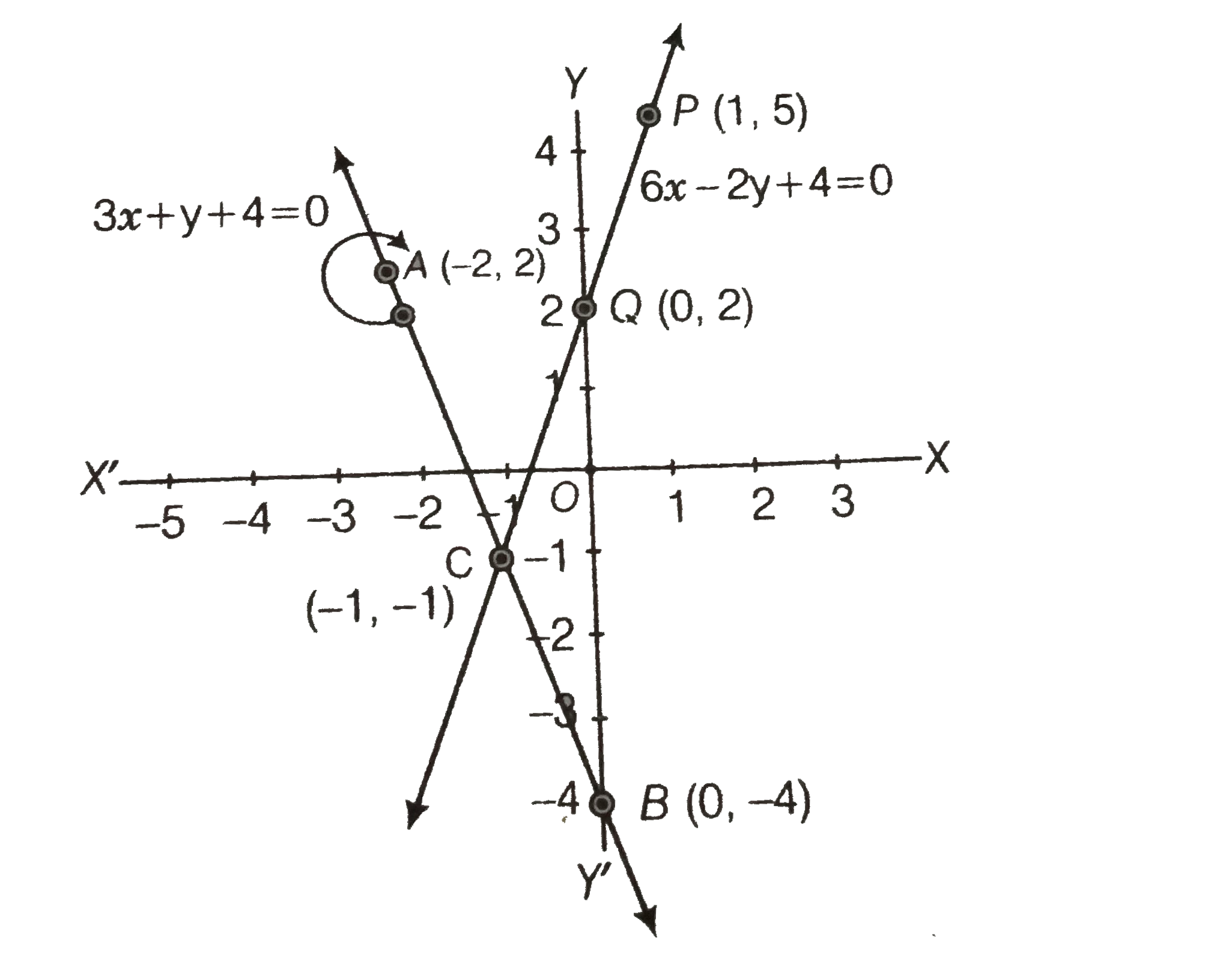(i) Given pair of equations is
3x+y+4=0` " " ...(i)`
and `" " 6x-2y+4=0 " " ...(ii)`
On comparing with `ax+by+c=0`, we get
`a_(1)=3, b_(1)=1`
and `c_(1)=4 " " `[from Eq. (i)]
`a_(2)=6, b_(2)=-2`
and `c_(2)=4 " "`[from Eq.(ii)]`
Here, `(a_(1))/(a_(2))=(3)/(6)=(1)/(2) , (b_(1))/(b_(2))=(1)/(-2)`
and `(c_(1))/(c_(2))=(4)/(4)=(1)/(1)`
`:' (a_(1))/(a_(2))!=(b_(1))/(b_(2))`
So, the given pair of linear equations are intersecting at one point, therefore these lines have unique solution.
Hence, given pair of linear equations is consistent.
We have, 3x+y+4=0
`rArr " " y=-4-3x`
when x=0, then y=-4 ltbr. when x=-1, then y=-1
When x=-2, then y=2
`{:(" "x,0,-1,-2),(" "y,-4,-1,2),("Points","B","C","A"):}`
and 6x-2y+4=0
`rArr 2y=6x+4`
`rArr y=3x+2`
When x=0, then y=2
When x=-1, then y=-1
When x=1, then y=5
`{:(" "x,-1,0,1),(" "y,-1,2,5),("Points","C","Q","P"):}`
Plotting the point B(0, -4) and A(-2, 2), we get the straight line AB. Plotting the points Q (0,2) and P(1,5), we get the straight line PQ. The lines AB and PQ intersect at C (-1, -1).
(ii) Given pair of equations is `" " x-2y=6 " " ...(i)`
and `" " 3x-6y=0 " " ...(ii)`
On comparing with a x + by + c =0. we get
`a_(1)=1, b_(1)=-2` and `c_(1)=-6 " " ` [from Eq. (i)]
`a_(2)=3, b_(2)=-6 ` and `c_(2)=0 ` [" from Eq." (ii)]
Here, `(a_(1))/(a_(2))=(1)/(3), (b_(1))/(b_(2))= (-2)/(-6)=(1)/(3) ` and `(c_(1))/(c_(2))=(-6)/(0)`
`:. " " (a_(1))/(a_(2))=(b_(1))/(b_(2))=(c_(1))/(c_(2))`
Hence, the lines represented by the given equations are parallel. Therefore, it has no solution. So, the given pair of lines is inconsistent.
(iii) Given pair of equation is `" " x+y=3 " " ...(i)`
and `" " 3x+3y=9 " " ...(ii)`
On comparing with ax+by+c=0. we get
`a_(1)=1, b_(1)` and `c_(1)=-3 " " ` [from Eq. (i)]
`a_(2)=3, b_(2)=3` and `c_(2)=-9 " " [from Eq. (ii)]
Here, `" " (a_(1))/(a_(2))=(1)/(3), (b_(1))/(b_(2))=(1)/(3)` and `(c_(1))/(c_(2))=(-3)/(-9)=(1)/(3)`
`rArr " " (a_(1))/(a_(2))=(b_(1))/(b_(2))=(c_(1))/(c_(2))`
So, the given pair of lines is coincident. Therefore, these lines have infinitely many solutions. Hence, the given pair of linear equations is consistent.
Now, `" " x+y=3 rArr y=3-x`
If x=0, then y=3, If x=3, then y=0
`{:(x,0,3,,),(y,3,0,,),("Points",A,B,,):}`
and `" " 3x+3y=9 rArr 3y = 9-3x`
`rArr " " y(9-3x)/(3)`
If x=0, then y=3, if x=1, then y=2 and if x=3, then y=0
`{:(x,0,1,3,),(y,3,2,0,),("Points",C,D,E,):}`
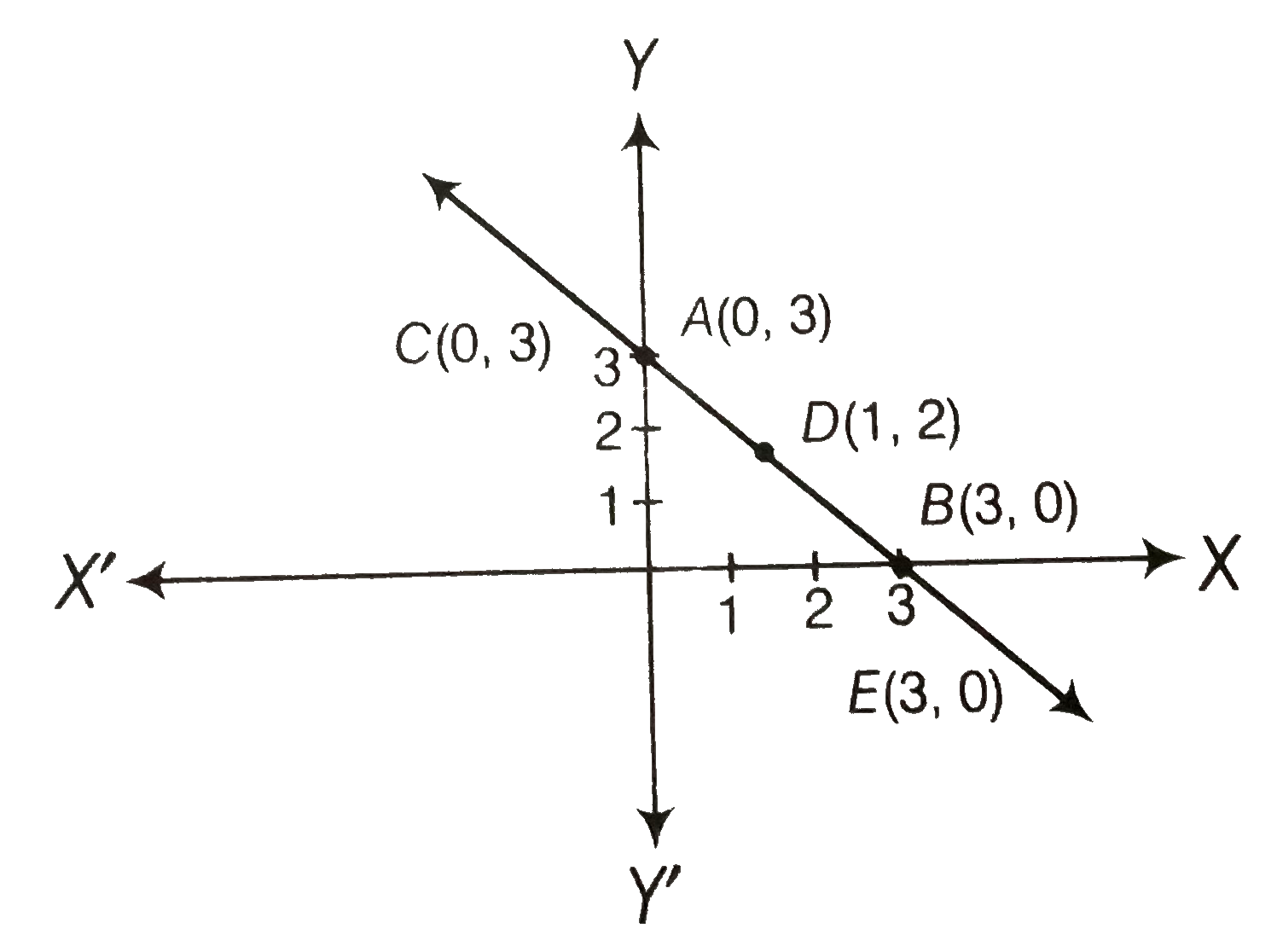
Plotting the points A (0,3) and B (3,0), we get the line AB. Again, plotting the points C(0,3)D(1,2) and E(3,0), we get the line CDE.
We observe that the lines represented by Eqa. (i) and (ii) are coincident.