Text Solution
Verified by Experts
Topper's Solved these Questions
CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)
CBSE COMPLEMENTARY MATERIAL|Exercise SECTION E|6 VideosCBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)
CBSE COMPLEMENTARY MATERIAL|Exercise SECTION B|6 VideosCBSE Examination Paper Delhi–2014
CBSE COMPLEMENTARY MATERIAL|Exercise SET-III (Questions Uncommon to set-I and II)|9 VideosDUAL NATURE OF MATTER AND RADIATION & ATOMS AND NUCLEI
CBSE COMPLEMENTARY MATERIAL|Exercise Long Answer Question|22 Videos
Similar Questions
Explore conceptually related problems
CBSE COMPLEMENTARY MATERIAL-CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)-SECTION C
- Name the parts of the electromagnetic spectrum which is suitable fo...
Text Solution
|
- Name the parts of the electromagnetic spectrum which is used to tre...
Text Solution
|
- Name the parts of the electromagnetic spectrum which is used as a d...
Text Solution
|
- A giant refracting telescope at an observatory has an objective lens o...
Text Solution
|
- (i) A giant refracting telescope at an observatory has an objective le...
Text Solution
|
- Write Einstein’s photoelectric equation and mention which important fe...
Text Solution
|
- In the study of Geiger-Marsdon experiment on scattering of a-particles...
Text Solution
|
- Distinguish between nuclear fission and fusion. Show how in both these...
Text Solution
|
- A cell of emf ‘E’ and internal resistance ‘r’ is connected across a va...
Text Solution
|
- Two capacitors of unknown capacitances C(1) and C(2) are connected...
Text Solution
|
- State the principle of working of a galvanometer. A galvanometer of...
Text Solution
|
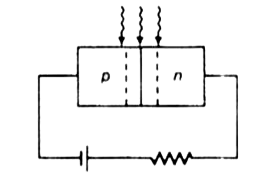
- With what considerations in view, a photodiode is fabricated ? State i...
Text Solution
|
- In double slit experiment using light of wavelength 600 nm, the angula...
Text Solution
|
- Answer the following questions: Light of wavelength 5000 A propagat...
Text Solution
|
- An inductor L of inductance X(L) is connected in series with a bulb B ...
Text Solution
|