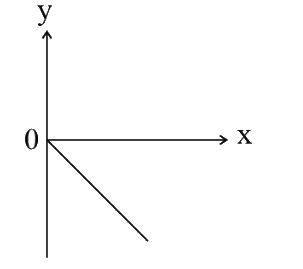
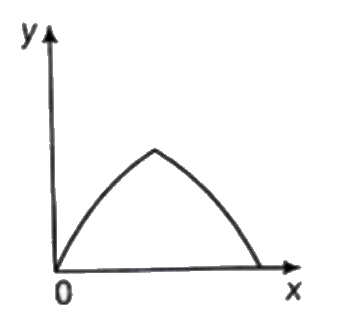
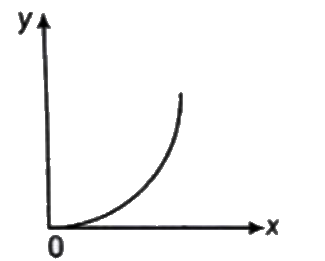
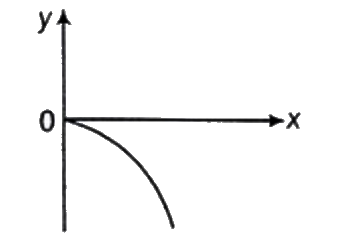
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NTA MOCK TESTS-NTA NEET SET 61-PHYSICS
- The ratio of minimum to maximum wavelength in Balmer series is
Text Solution
|
- Two particles of mass m and 2m have their position vectors as a functi...
Text Solution
|
- A particle of mass m rotates in a circle of radius a with uniform angu...
Text Solution
|
- The velocity-time graph of a particle moving along a straight line is ...
Text Solution
|
- If a wire of resistance R is melted and recasted in to half of its len...
Text Solution
|
- The conducting circular loops of radii R(1) and R(2) are placed in the...
Text Solution
|
- The magnitude and direction of the electric field at point P can be be...
Text Solution
|
- Two balls of radius r each are placed at a distance R and released . T...
Text Solution
|
- A black body of temperature T is inside a chamber of temperature T(0) ...
Text Solution
|
- For the adiabatic expansion of a perfect monoatomic gas, when volume i...
Text Solution
|
- A charged particle moving in a uniform magnetic field penetrates a lay...
Text Solution
|
- A boat which has a speed of 5 km// hr in steel water crosses a river...
Text Solution
|
- A cyclist turns around a curve at 15 miles/hour. If he turns at double...
Text Solution
|
- If a simple pendulum oscillates with an amplitude of 50 mm and time pe...
Text Solution
|
- In photoelectric emission process from a metal of work function 1.8 eV...
Text Solution
|
- The SI unit of the coefficent of viscosity is
Text Solution
|
- A ray of light travelling in the direction 1/2 (hati+sqrt(3)hatj) is i...
Text Solution
|
- A cylinder is rolling down on a inclined plane of inclination60^(@). W...
Text Solution
|
- A transistor is used as a common emitter amplifier with a load resista...
Text Solution
|
- A point near the equator has: (H and V are horizontal and vertical com...
Text Solution
|