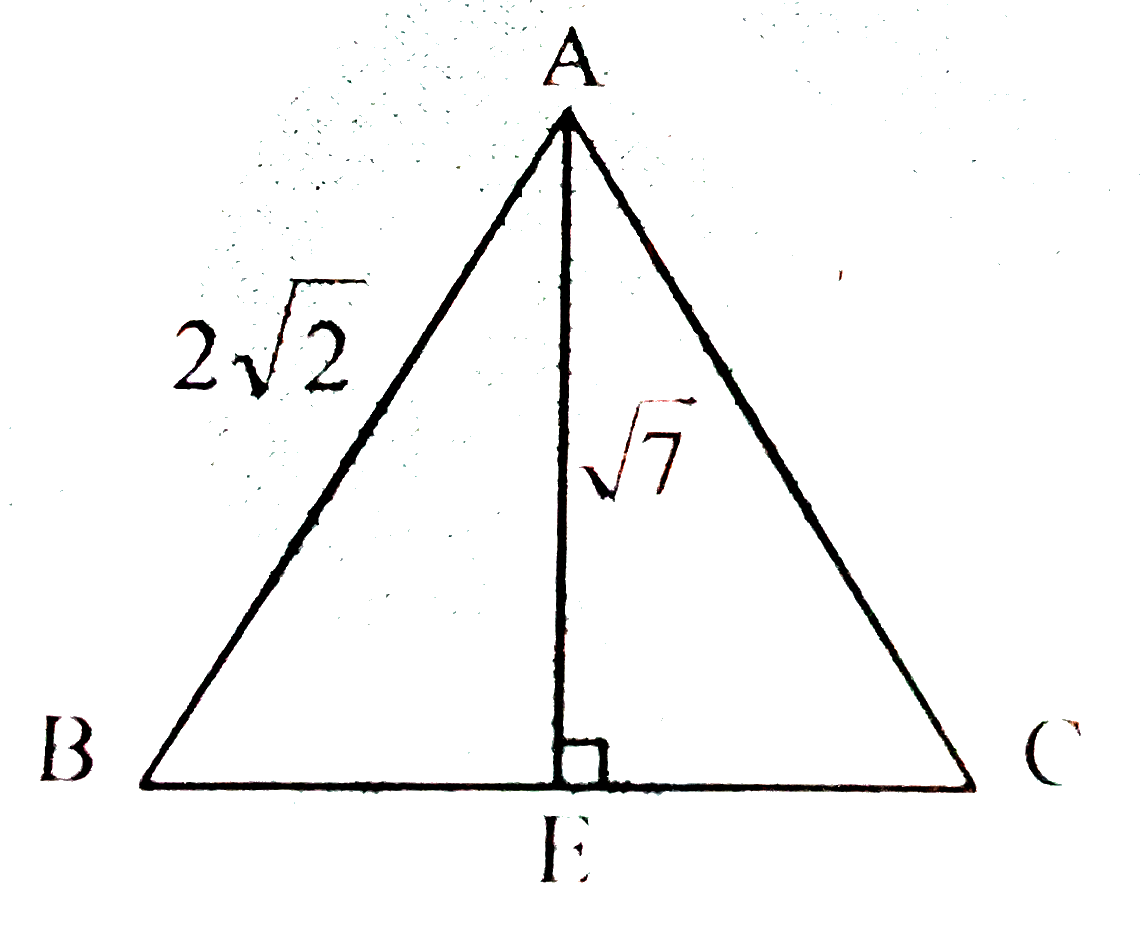A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
KVPY PREVIOUS YEAR-KVPY-PART-2 MATHEMATICS
- Let a, b, c be positive integers such that (asqrt2+b)/(bsqrt2+c) is a ...
Text Solution
|
- The number of solutions (x, y, z) to the system of equations x+2y+4z...
Text Solution
|
- In a triangle ABC, it is known that AB=AC. Suppose D is the mid-point ...
Text Solution
|
- A train leaves Pune at 7 :30 am and reaches Mumbai at 11 : 30 am. Anot...
Text Solution
|
- In the adjacent figures, which has the shortest path-
Text Solution
|