Text Solution
Verified by Experts
Topper's Solved these Questions
GRAVITATION
SUBHASH PUBLICATION|Exercise FIVE MARKS QUESTIONS WITH ANSWERS|7 VideosGRAVITATION
SUBHASH PUBLICATION|Exercise NUMERICALS WITH SOLUTIONS|15 VideosGRAVITATION
SUBHASH PUBLICATION|Exercise TWO MARKS QUESTIONS WITH ANSWERS|5 VideosANNUAL EXAMINATION QUESTION PAPER WITH ANSWER SOUTH 2019
SUBHASH PUBLICATION|Exercise PART-D|9 VideosKINETIC THEORY
SUBHASH PUBLICATION|Exercise NUMERICALS WITH SOLUTIONS|19 Videos
Similar Questions
Explore conceptually related problems
SUBHASH PUBLICATION-GRAVITATION -THREE MARKS QUESTIONS WITH ANSWERS
- Write a few characteristics of gravitational force.
Text Solution
|
- Show that the area swept by a planet in a given interval time is const...
Text Solution
|
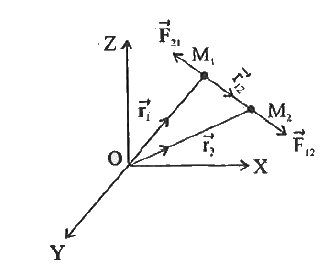
- If vec(r(1)) and vec(r(2)) are the position vectors of mass bodies M(...
Text Solution
|
- Show the g=(GM)/(R^(2))
Text Solution
|
- Obtain an expression for the average density of the Earth.
Text Solution
|
- Show that V(0) =sqrt(gr)
Text Solution
|
- Arrive at the expression for escape speed of the body from the surface...
Text Solution
|