Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT-LINES AND ANGLES-Exercise 6.1
- In Fig. 6.16, if x+y=w+z, then prove that AOB is a line.
Text Solution
|
- In Fig. 6.13, lines AB and CD intersect at O. If /A O C\ +/B O E=70^@...
Text Solution
|
- In fig: 6.14, lines XY and MN intersect at O. If /P O Y=90^@and a : b...
Text Solution
|
- In Fig. 6.15, /P Q R=/P R Q, then prove that /P Q S=/P R T.
Text Solution
|
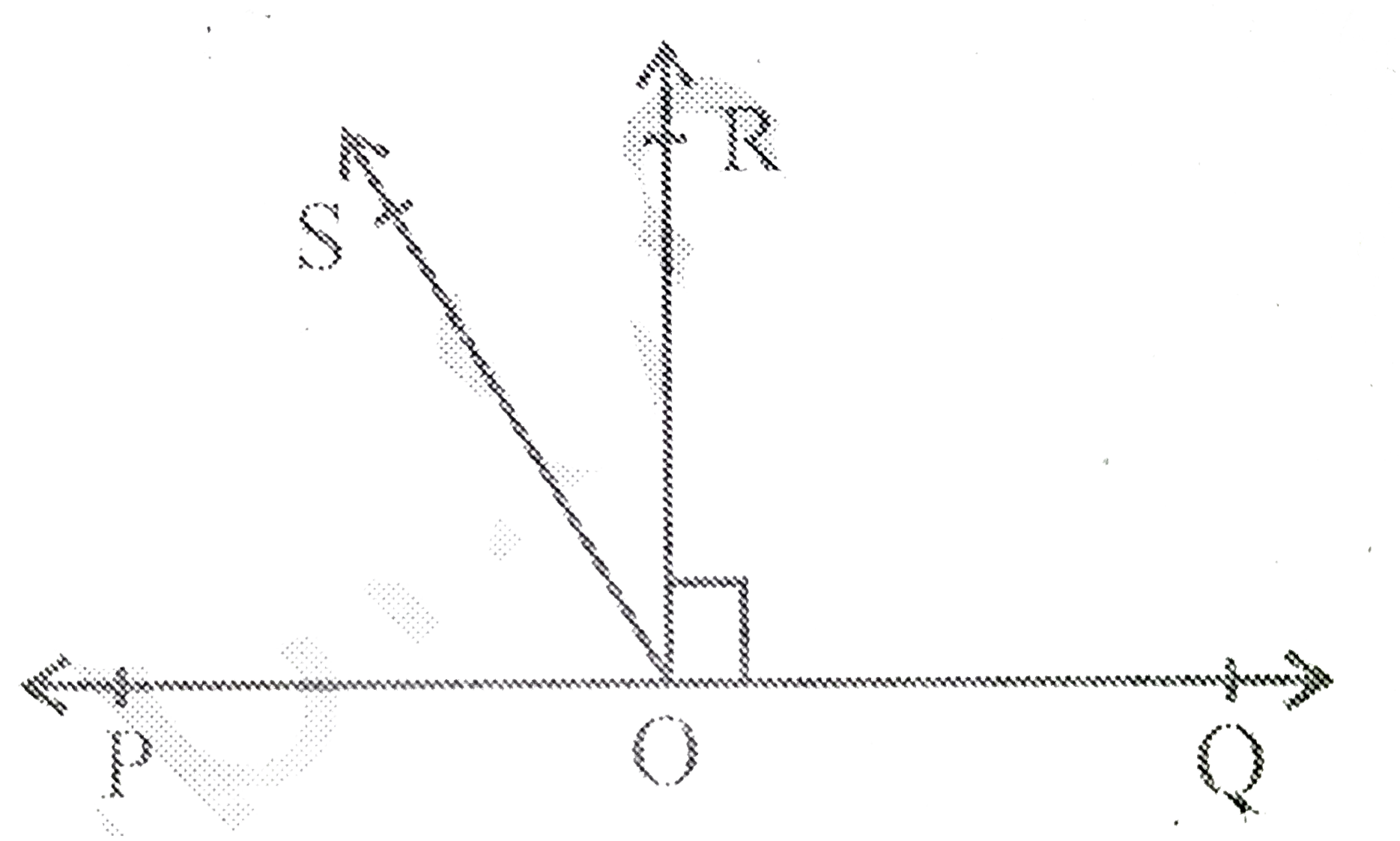
- In Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS i...
Text Solution
|
- It is given that /X Y Z=64^@ and XY is produced to point P. Draw a fig...
Text Solution
|