Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SURFACE AREAS AND VOLUMES
CPC CAMBRIDGE PUBLICATION|Exercise EXERCISE 15.3|9 VideosSURFACE AREAS AND VOLUMES
CPC CAMBRIDGE PUBLICATION|Exercise EXERCISE 15.4|5 VideosSURFACE AREAS AND VOLUMES
CPC CAMBRIDGE PUBLICATION|Exercise EXERCISE 15.4|5 VideosSTATISTICS
CPC CAMBRIDGE PUBLICATION|Exercise Exercise 13.4|4 VideosTRIANGLES
CPC CAMBRIDGE PUBLICATION|Exercise Exercise 2.6 (Optional)|8 Videos
Similar Questions
Explore conceptually related problems
CPC CAMBRIDGE PUBLICATION-SURFACE AREAS AND VOLUMES -EXERCISE 15.2
- A solid in the shape of a cone standing on a hemisphere with both the...
Text Solution
|
- Rachel, an engineering student, was asked to make a model shaped like...
Text Solution
|
- A gulab jamun, contains sugar syrup up to about 30% of its volume. Fin...
Text Solution
|
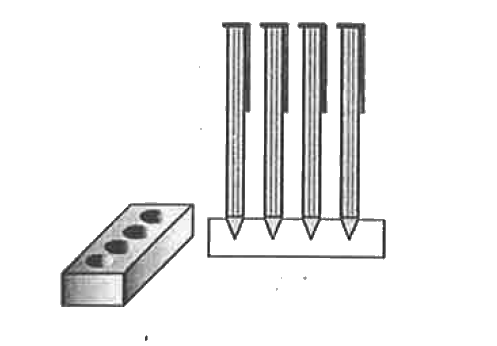
- A pen stand made of wood is in the shape of a cuboid with four conical...
Text Solution
|
- A vessel is the from of an inverted cone. Its height is 8 cm and the ...
Text Solution
|
- A solid iron pole consists of a cylinder of a height 220cm and base ...
Text Solution
|
- A solid consisting of a right circular cone of height 120cm and radiu...
Text Solution
|
- A spherical glass vessel has a cylindrical neck 8cm long, 2cm in di...
Text Solution
|