The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively ` 120^(@) and 40^(@)` . Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe ?

Explanation

Let the lengths of the corresponding arc be `l_(1) and l_(2)` .
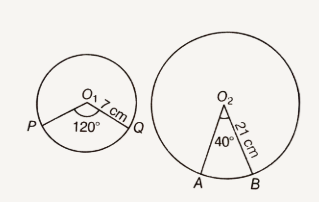
Given that, radius of sector `PO_(1)QP` = 7 cm
and radius of sector `AO_(2)BA = 21 cm`
Central angle of the sector `PO_(1)QP = 120^(@)`
and central angle of the sector `AO_(2)BA = 40^(@)`
= `(pir^(2))/(360^(@))xxtheta= (pi(7)^(2))/(360^(@))xx120^(@)`
= `(22)/(7)xx(7xx7)/(360^(@))xx120`
= `(22xx7)/(3)=(154)/(3)cm^(2)`
and area of the sector with central angle `O_(2)`
=`(pir^(2))/(360^(@))xxtheta=(pi(21)^(2))/(360^(@))xx40^(@)`
=`(22)/(7)xx(21xx21)/(360^(@))xx40^(@)`
= `(22xx3xx21)/(9) = 22xx7 = 154 cm^(2)`
Now, corresponding arc length of the sector `PO_(1)QP`
= Central angle `xx` Radius of the sector
=`120^(@)xx7xx(pi)/(180^(@))` [`because theta= (l)/(r) and 1^(@) = (pi)/(180^(@))R`]
= `(2)/(3) xx7xx(22)/(7)`
= `(44)/(3)cm`
and corresponding arc lengh of the sector `AO_(2)BA`
Central angle `xx` Radius of the sector
=`40^(@)xx21xx(pi)/(180^(@))`[`:. theta= (l)/(r) and 1^(@) = (pi)/(180^(@))R`]
= ` (2)/(9)xx21xx(22)/(7)`
= `(2)/(3)xx22=(44)/(3)cm`
Hence, we observe that arc length of two sectors of two different circles may be equal but their area need not be equal.