Home
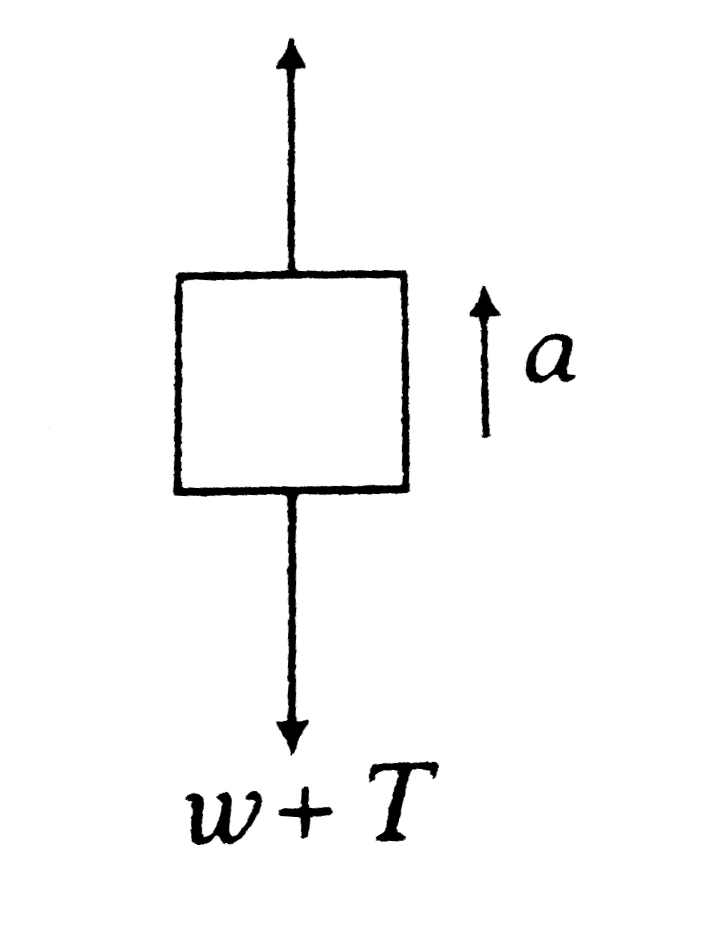
Class 11
PHYSICS
A spherical ball of radius 3xx10^(-4)m a...

A spherical ball of radius `3xx10^(-4)`m and density `10^(4)kg//m^(3)` falls freely under gravity through a distance h before entering a tank of water. If after entering the water the velocity of the ball does not change, find h the viscosity of water is `9.8xx10^(-6)N-s//m^(2)`

A

`1.65xx10^(3)m`

B

`2.65xx10^(2)m`

C

`3.65xx10^(4)m`

D

`1.45xx10^(2) m`

Text Solution

Verified by Experts

The correct Answer is:
A
Before entering the water the velocity of ball is `sqrt(2gh)`. If after entering the water this velocity does not change, then this value should be equal to the terminal velocity. Therefore,
`sqrt(2gh)=(2)/(9)(r^(2)(rho-sigma)g)/(eta)`
`therefore h=({(2)/(9)(r^(2)(rho-sigma)g)/(eta)}^(2))/(2g)=(2)/(81)xx(r^(4)(rho-sigma)^(2)g)/eta^(2)`
`=(2)/(81)xx((3xx10^(-4))^(4)(10^(4)-10^(3))^(2)xx9.8)/((9.8xx10^(-6))^(2))=1.65xx10^(3)m`
Promotional Banner

Topper's Solved these Questions

  • FLUID MECHANICS

    DC PANDEY|Exercise Check point 13.4|10 Videos

  • FLUID MECHANICS

    DC PANDEY|Exercise Taking it together|157 Videos

  • FLUID MECHANICS

    DC PANDEY|Exercise Check point 13.2|10 Videos

  • EXPERIMENTS

    DC PANDEY|Exercise Subjective|15 Videos

  • GENERAL PHYSICS

    DC PANDEY|Exercise INTEGER_TYPE|2 Videos

Similar Questions

Explore conceptually related problems

A spherical ball of radius 3.0xx10^(-4) m and density 10^(4)(kg)/(m^(3)) falls freely under gravity through a distance H=nxx500m before entering a tank of water. If after enerting the water the velocity of the ball does not change, then find n. viscosity of water is 10xx10^(-6)(N-s)/(m^(2)) , g=10(m)/(s)

A small ball of radius 'r' falls freely under gravity through a distance 'h' before entering a tank of water. If after entering the water, the velocity of ball does not change, the 'h' is proportional to

A small ball of radius 'r' falls freely under gravity through a distance 'h' before entering a tank of water. If after entering the water, the velocity of ball does not change, the 'h' is proportional to

A metal ball ofradius 10^(-4) m and density 10^4 kg//m^3 falls freely under gravity through a distance 'h' and enters a tank of water. It is found that after entering the water, the velocity of ball does not change. What is the value of h? [eta "for water "10^(-5)" Pas ",g=10m//s^2" and "orh_("water")=10^3kg//m^3 ]

A ball of radius r and density r falls freely under gravity through a distance h before entering water. Velocity of ball does not change even on entering water. If viscosity of water is eta the value of h is given by

In an experiment to verify Stokes law , a small spherical ball of radius r and density rho falls under gracvity throught a distance h in air before entering a tank of wate . If the terminal velocity of the ball inside water is same as its velocity just befor entering the water surface , then the value of h is proportional to : ( ignore viscosity of air ) .

A metallic sphere of radius 1.0 xx 10^(-3) m and density 1.0 xx 10^(4) kg//m^(3) enters a tank of water, after a free fall through a distance of h in the earth's gravitational field. If its velocity remains unchanged after entering water, determine the value of h . Given: coefficient of viscosity of water = 1.0 xx 10^(-3) N s//m^(2), g = 10ms^(-12) and density of water = 1.0 xx 10^(3) kg//m^(3) .

A drop of radius 2xx10^(-5) and density 1.2xx10^(3)kg//m^(3) falls through air. The viscosity of air is 1.8xx10^(-5) N s//m^(2). Neglecting buoyancy due to air, the terminal speed of the drop is

A sphere of radius 10cm and density 500kg//m^(3) is under water of density 1000kg//m^(3) The acceleration of the sphere is 9.80m//s^(2) upward viscosity of water is 1.0 centipoise if g=9.81m//s^(2) the velocity of the sphere is