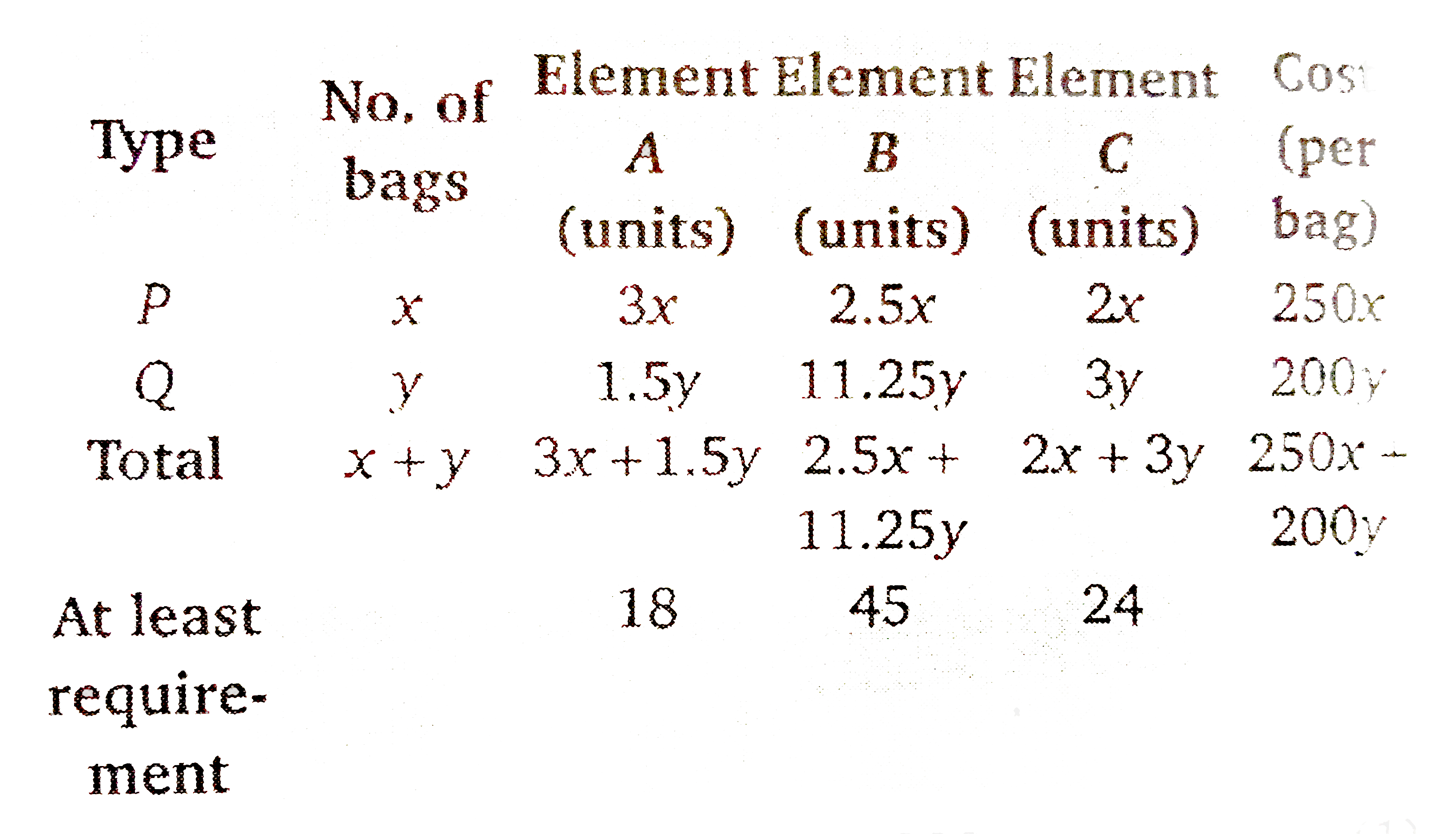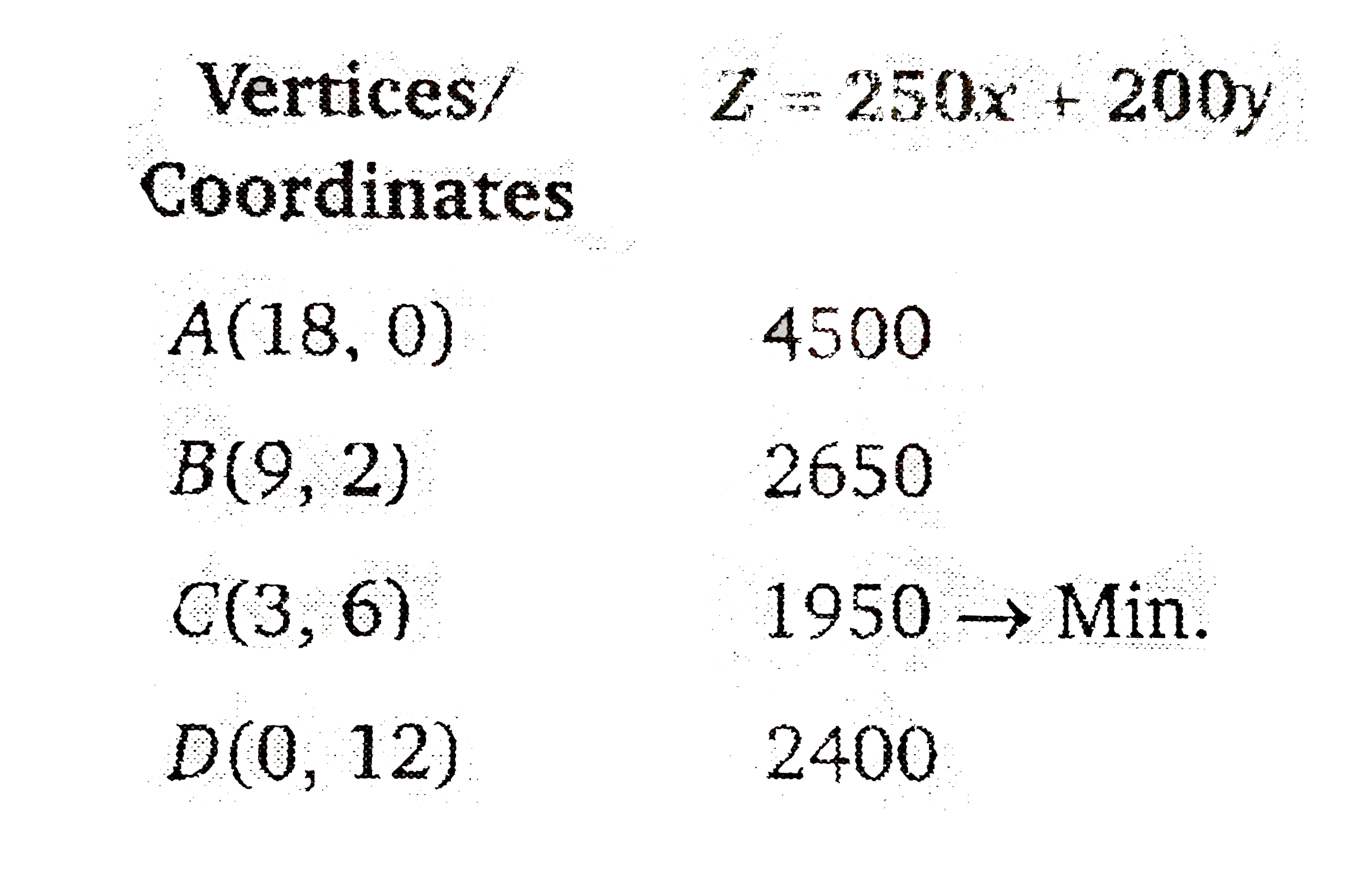Text Solution
Verified by Experts
NAGEEN PRAKASHAN-LINEAR PROGRAMMING-Miscellaneous Exercise
- (Diet problem) A dietician has to develop a special diet using two foo...
Text Solution
|
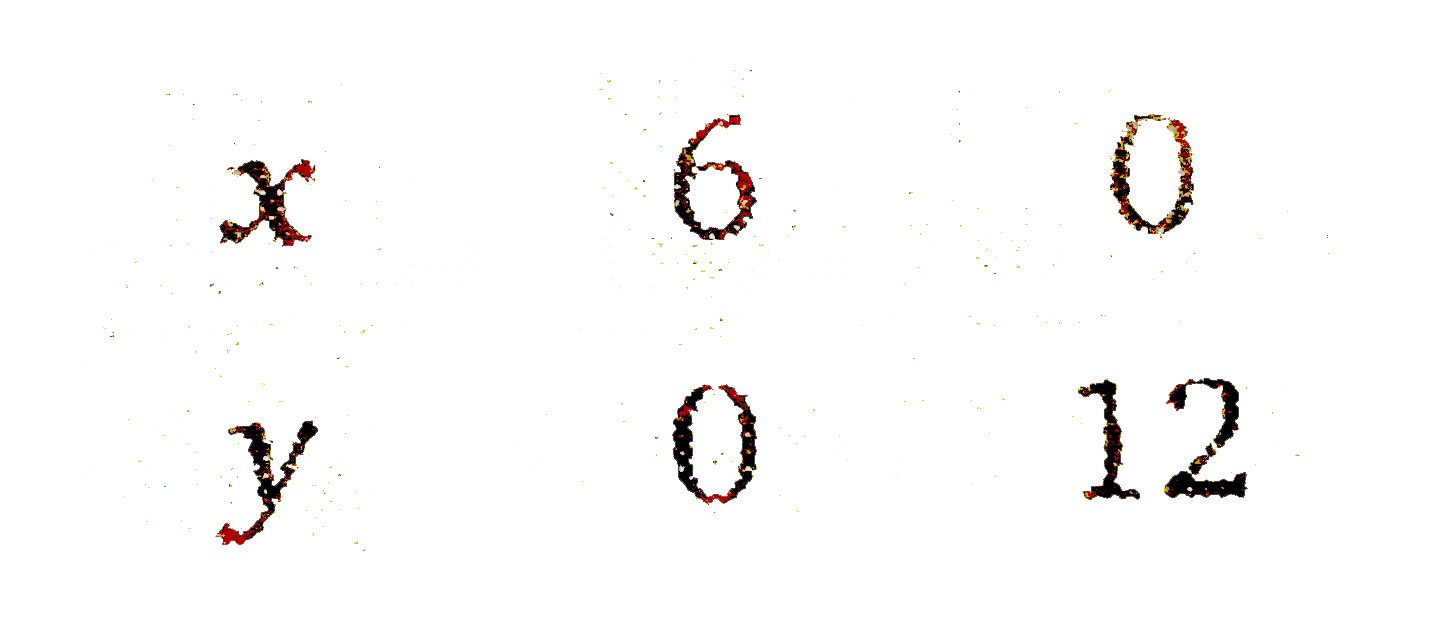
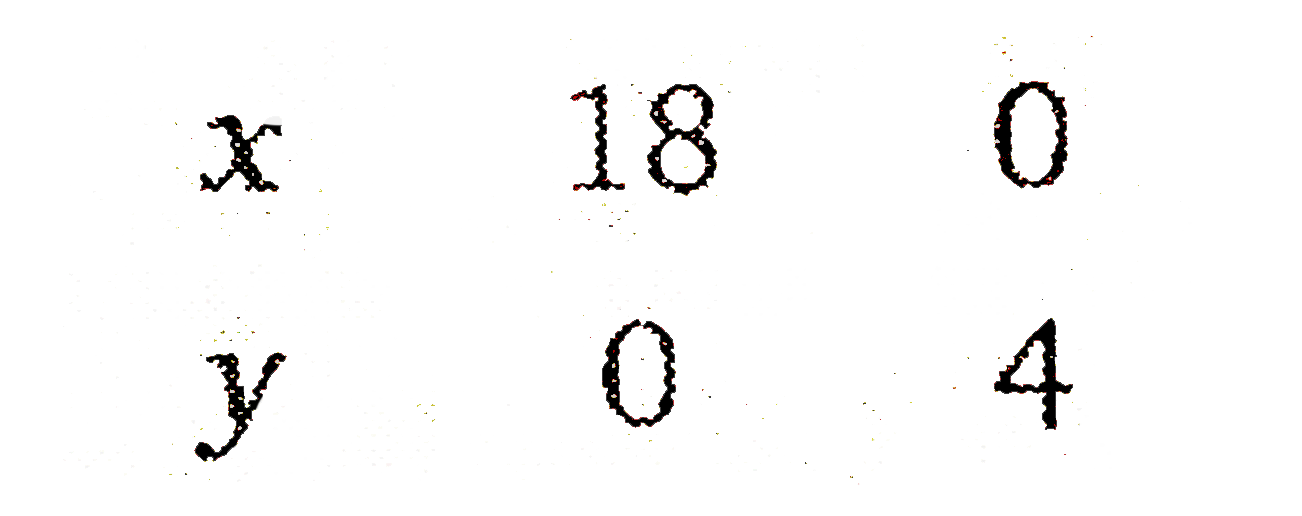
- A farmer mixes two brands P and Q of cattle feed. Brand P costing Rs. ...
Text Solution
|
- A dietician wishes to mix together two kinds of food X and Y in such a...
Text Solution
|
- A manufacturer makes two types of toys A and B. Three machines are ne...
Text Solution
|
- An aeroplane can carry a maximum of two passengers. A profit of Rs. 10...
Text Solution
|
- Two godowns A and B have grain capacity of 100 quintals and 50 qunital...
Text Solution
|
- An oil company has two depots A and B with capacities of 7000L and 400...
Text Solution
|
- A fruit grower canuse two types of fertilizer in his garden brand P an...
Text Solution
|
- A toy company manufactures two types of dolls A and B. Market research...
Text Solution
|