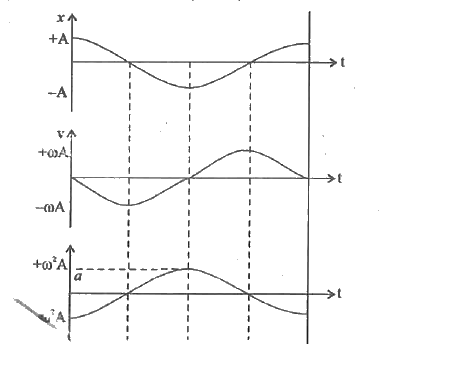
Text Solution
Verified by Experts
Topper's Solved these Questions
OSCILLATIONS
SUBHASH PUBLICATION|Exercise NUMERICALS WITH SOLUTIONS|41 VideosOSCILLATIONS
SUBHASH PUBLICATION|Exercise THREE MARKS QUESTIONS WITH ANSWERS|2 VideosMOTION IN PLANE
SUBHASH PUBLICATION|Exercise NUMERICALS WITH SOLUTIONS|47 VideosPHYSICAL WORLD
SUBHASH PUBLICATION|Exercise TWO MARKS QUESTIONS WITH ANSWERS|30 Videos
Similar Questions
Explore conceptually related problems
SUBHASH PUBLICATION-OSCILLATIONS-FIVE MARKS QUESTIONS WITH ANSWERS
- Arrive an expression for time period of simple pendulum.
Text Solution
|
- Give the expression for the amplitude of a damped oscillation of a par...
Text Solution
|
- Given displacement of a particle executing SHM y(t)=A cos (omegat+phi)...
Text Solution
|
- Arrive at the expression for time period of oscillation of a mass atta...
Text Solution
|