Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROMAGNETIC INDUCTION
SUBHASH PUBLICATION|Exercise NUMERICALS WITH SOLUTIONS|19 VideosELECTROMAGNETIC INDUCTION
SUBHASH PUBLICATION|Exercise THREE MARKS QUESTIONS WITH ANSWERS|6 VideosELECTRIC CHARGES AND FIELDS
SUBHASH PUBLICATION|Exercise NUMERICALS WITH SOLUTIONS|21 VideosELECTROMAGNETIC WAVES
SUBHASH PUBLICATION|Exercise ONE MARK QUESTIONS WITH ANSWERS|36 Videos
Similar Questions
Explore conceptually related problems
SUBHASH PUBLICATION-ELECTROMAGNETIC INDUCTION-FIVE MARKS QUESTIONS WITH ANSWERS
- Describe expriments to demonstrate electromagnetic induction.
Text Solution
|
- What is meant by alternating current ? Derive the expression for a sin...
Text Solution
|
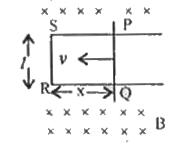
- Derive the expression for emf induced in a straight conductor moving p...
Text Solution
|
- Obtain an expression for energy stored in an inductor connected to a s...
Text Solution
|