Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT-TRIANGLES-SOLVED EXAMPLES
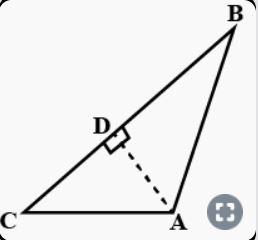
- In figure/A C B=90^@and C D|A B. Prove that (B C^2)/(A C^2)=(B D)/(A D...
Text Solution
|
- A ladder is placed against a wall such that its foot is at a distance...
Text Solution
|
- In fig., if A D|B C, prove thatA B^2+C D^2=B D^2+A C^2.
Text Solution
|
- BL and CM are medians of a triangle ABC right angled at A. Prove that...
Text Solution
|
- O is any point inside a rectangle ABCD. Prove that O B^2+O D^2=O A^2+...
Text Solution
|
- In Figure (P S)/(S Q)=(P T)/(T R)and /P S T=/P R Q. Prove that PQR i...
Text Solution
|
- ABCD is a trapezium with AB || DC. E and F are points on non-parallel...
Text Solution
|
- A girl of height 90 cm is walking away from the base of a lamp-post a...
Text Solution
|
- In Figure the line segment XY is parallel to side AC of DeltaA B Cand...
Text Solution
|
- In figure Cm and RN are respectively the medians of DeltaA B Cand De...
Text Solution
|
- Observe and then find /P.
Text Solution
|
- If a line intersects sides AB and AC of a DeltaA B Cat D and E respect...
Text Solution
|
- In figure, if PQ||RS, prove that DeltaP O Q DeltaS O R.
Text Solution
|
- In figure OA**O B=O C** O D. Show that /A=/Cand /B=/D.
Text Solution
|