Text Solution
Verified by Experts
Topper's Solved these Questions
CIRCLES
NAGEEN PRAKASHAN|Exercise Exercise|25 VideosCIRCLES
NAGEEN PRAKASHAN|Exercise Revision Exercise Very Short Answer Question|7 VideosCIRCLES
NAGEEN PRAKASHAN|Exercise Revision Exercise Long Answer Questions|3 VideosARITHMETIC PROGRESSION
NAGEEN PRAKASHAN|Exercise Revision Exercise Long Answer Question|5 VideosCO-ORDINATE GEOMETRY
NAGEEN PRAKASHAN|Exercise Revision Exercise Short Answer Questions|9 Videos
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN-CIRCLES-Problems From NCERT/exemplar
- Two concentric circles are of radii 5 cm and 3 cm. Find the length ...
Text Solution
|
- If a,b,c are the sides of a right triangle , where c is the hypotenuse...
Text Solution
|
- X Yand XprimeYprimeare two parallel tangents to a circle with centre ...
Text Solution
|
- A triangle ABC is drawn to circumscribe a circle of radius 4 cm such...
Text Solution
|
- If AB is chord of a circle with centre O, AOC is a diameter and AT is ...
Text Solution
|
- Two circles with centres O and O' of radii 3 cm and 4 cm, respectively...
Text Solution
|
- AB is a diameter of a circle and AC is its chord such that angleBAC=30...
Text Solution
|
- In figure, AB is a chord of the circle and AOC is the diameter such th...
Text Solution
|
- In figure, if 0 is the centre of a circle, PQ is a chord and the tange...
Text Solution
|
- If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF=BC+...
Text Solution
|
- In figure, tangents PQ and PR are drawn to a circle such that angleRPQ...
Text Solution
|
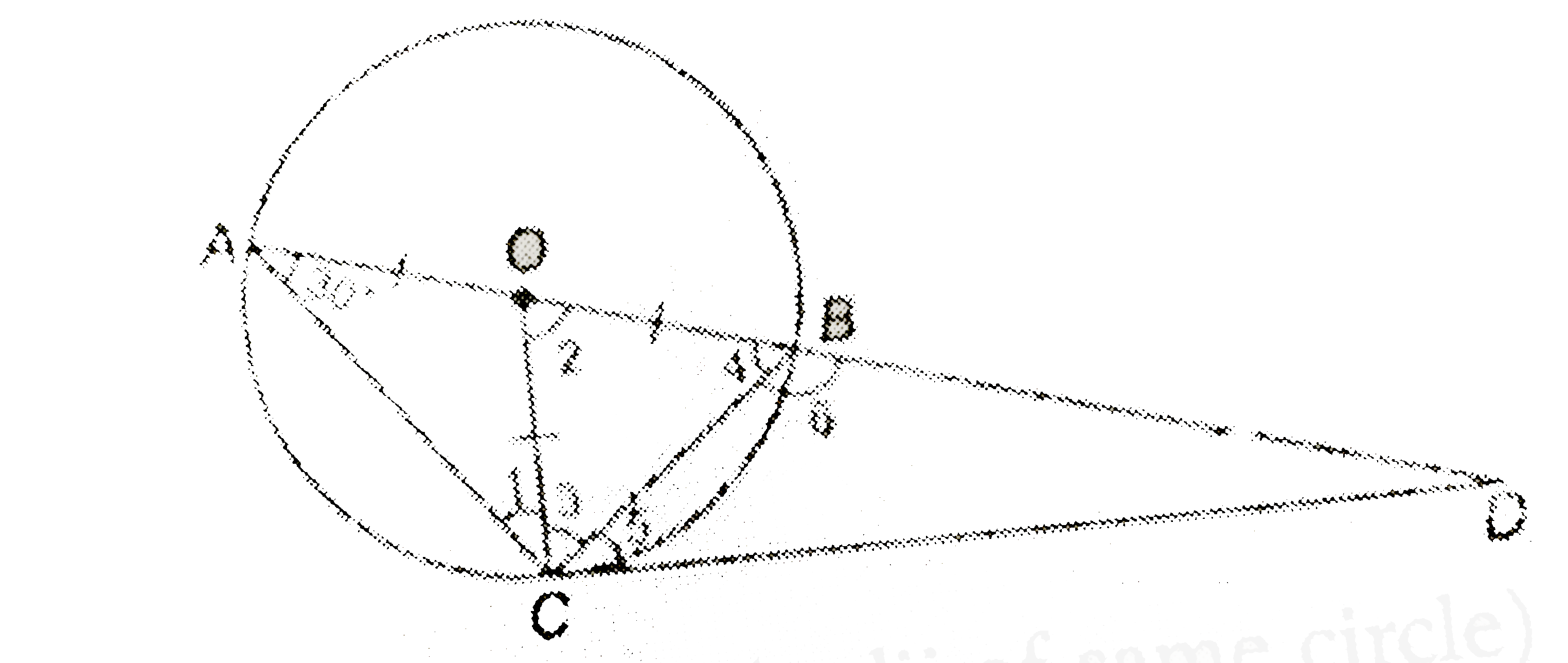 Hence Proved.
Hence Proved.