Home
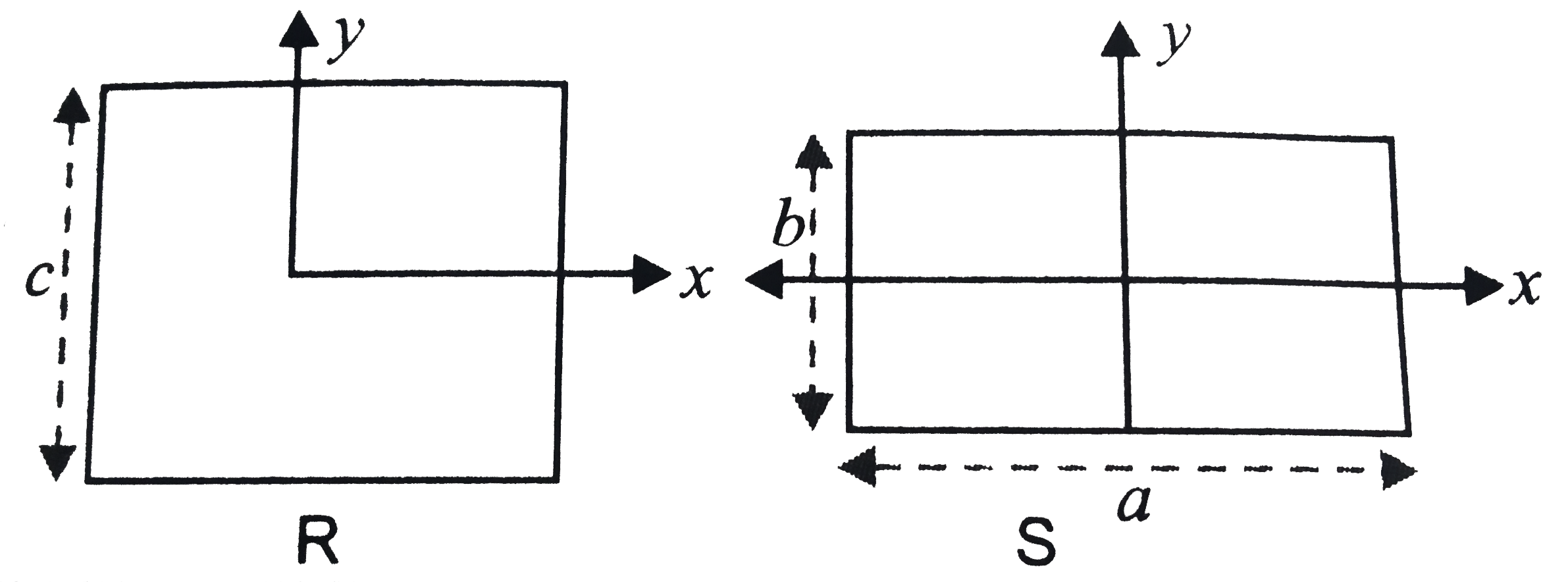
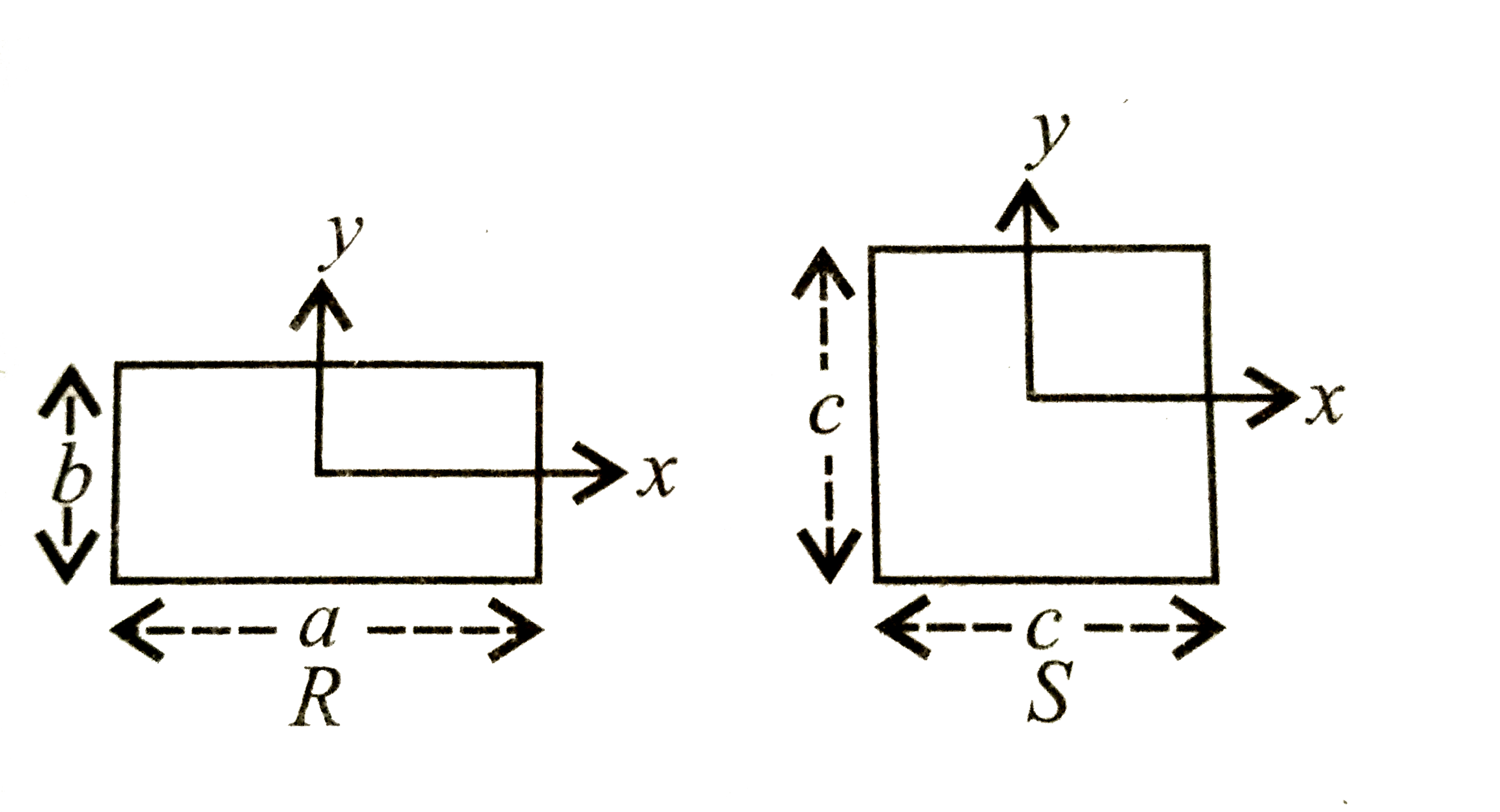
Class 11
PHYSICS
A uniform square plate S (side c) and a ...

A uniform square plate `S (side c)` and a uniform rectangular plate `R(side b,a)` have identical areas and mass [Fig.]
Show that
(i) `I_(xR)//I_(xS) lt 1`, (ii) `I_(yR)//I_(yS) gt 1`, (iii) `I_(zR)//I_(zS) gt 1`.

A

(i) only

B

(ii) only

C

Both (i) and (ii)

D

Neither (i) nor (ii)

Text Solution

Verified by Experts

The correct Answer is:
C
As, areaof rectangular plate R= Area of square plate S
`therefore a xx b =c^(2)`
i) `(I_(x)R)/(I_(x)S)=b^(2)/c^(2)=b/a`
As `b lt a therefore (I_(x)R)/(I_(x)S) lt 1`
ii) `(I_(y)R)/(I_(y)S) = a^(2)/c^(2)=a/b`
As `a gt b therefore (I_(y)R)/(I_(y)S) gt 1`
Promotional Banner

Topper's Solved these Questions

  • SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS

    NCERT FINGERTIPS|Exercise Kinematics Of Rotational Motion About A Fixed Axis|3 Videos

  • SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS

    NCERT FINGERTIPS|Exercise Dynamics Of Rotational Motion About A Fixed Axis|10 Videos

  • SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS

    NCERT FINGERTIPS|Exercise Moment Of Inertia|7 Videos

  • PRACTICE PAPERS

    NCERT FINGERTIPS|Exercise Practice Paper 3|50 Videos

  • THERMAL PROPERTIES OF MATTER

    NCERT FINGERTIPS|Exercise Assertion And Reason|10 Videos

Similar Questions

Explore conceptually related problems

A unifrom square plate S (side c) and a unifrom rectangular plate R(side b,a) have identical areas and mass [Fig.] Show that (i) I_(xR)//I_(xS) lt 1 , (ii) I_(yR)//I_(yS) gt 1 , (iii) I_(zR)//I_(zS) gt 1 .

The moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through the centre O and perpendicular to the plane of the plate is (a) I_(1)+I_(2) , (b) I_(2)+I_(4) 2I_(1)+I_(3) , (d) I_(1)+2I_(3)

The moment of inertia of thin square plate ABCD of uniform thickness about an axis passing through the center O and perpendicular to the plane of the plate is ( i ) I_(1)+I_(2) ( ii ) I_(2)+I_(4) ( iii ) I_(1)+I_(3) ( iv ) I_(1)+I_(2)+I_(3)+I_(4) where I_(1) , I_(2) , I_(3) and I_(4) are repectively moments of inertia about axes 1 , 2 , 3 and 4 which are in the plane of the plane

Prove that : (i) " adj " I=I (ii) " adj " O=O (iii) I^(-1)=I .

Let I_(1) and I_(2) be the moment of inertia of a uniform square plate about axes shown in the figure. Then the ratio I_(1):I_(2) is

Find the moment of inertia of a uniform rectangular plate of mass M and edges of length 'I' and 'b' about its axis passing through the centre and perpendicular to it.

The magnitude of gratitational field intensities at distance r_(1) and r_(2) from the centre of a uniform solid sphere of radius R and mass M are I_(1) and I_(2) respectively. Find the ratio of I_(1)//I_(2) if (a) r_(1) gt R and r_(2) gt R and (b) r_(1) lt R and r_(2) lt R (c ) r_(1) gt R and r_(2) lt R .

Consider a uniform square plate shown in the figure. I_(1), I_(2), I_(3) and I_(4) are moment of inertia of the plate about the axes 1, 2, 3 and 4 respectively. Axes 1 and 2 are diagonals and 3 and 4 are lines passing through centre parallel to sides of the square. The moment of inertia of the plate about an axis passing through centre and perpendicular to the plane of the figure is equal to which of the followings. (a) I_(3) + I_(4) (b) I_(1) + I_(3) (c) I_(2) + I_(3) (d) (1)/(2) (I_(1) + I_(2) + I_(3) + I_(4))

The ionization potential values of an element are in the following order I_(1) lt I_(2) lt lt lt lt I_(3) lt I_(4) lt I_(5) . The element is