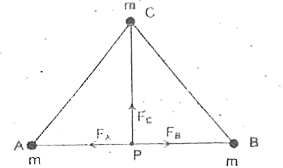
Using the superposition principle, the net gravitational force on `P` is `vecF=vecF_(A)+vecF_(B)+vecF_(C )`
`(a)` As shown in the figure, when `P` is at the mid point of a side, `vecF_(A)` and `vecF_(B)` will be equal in magnitude but opposite in direction. Hence they will cancel each other. So the net force on the particle `P` will be the force due to the particle placed at `C` only.
`impliesF=F_(C )=G.(m.m)/((CP)^(2))=G(m^(2))/((a sin 60^(@))^(2))=(4)/(3)(Gm^(2))/(a^(2))"along" PC`.
`(b)` At the centre of the triangle `O`, the forces `vecF_(A)`, `vecF_(B)` and `vecF_(C )` will be equal in magnitude and will subtend `120^(@)` with each other. Hence the resultant force on `P` at `O` is `vecF=vecF_(A)+vecF_(B)+vecF_(C )=O`.