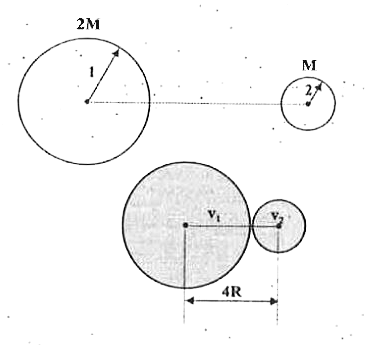
Taking both the bodies as a system, from conserving momentum of the system
`m_(1)v_(1)-m_(2)v_(2)=0implies(m_(1))/(m_(2))=(v_(2))/(v_(1))=2`
again , if the accelerations are `a_(1)` and `a_(2)`, the net external force on the system `=0`
`impliesveca_(CM)=0impliesm_(1)a_(1)-m_(2)a_(2)=0`
`(m_(1))/(m_(2))=(a_(2))/(a_(1))=2`
Now conserving the total mechanical energy, we have
`-(G(2M)M)/(16R)=-(G(2M)M)/(4R)+(1)/(2)(2M)v_(1)^(2)+(1)/(2)(M)v_(2)^(2)`
`v_(1)=sqrt((GM)/(8R))`, `v_(2)=2sqrt((GM)/(8R))`
Note : The velocities and accelerations are w.r.t. the inertial reference frame (i.e. the centre of mass of the system).