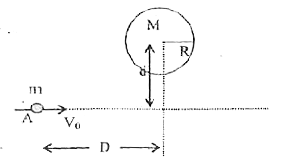
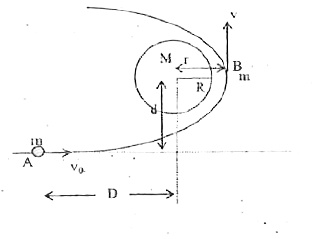
Text Solution
Verified by Experts
Topper's Solved these Questions
GRAVITATION
FIITJEE|Exercise Solved problem (Objective)|15 VideosGRAVITATION
FIITJEE|Exercise Comprehension|13 VideosGRAVITATION
FIITJEE|Exercise Numerical based Question|2 VideosGMP ASSESMENT
FIITJEE|Exercise Numerical Based|61 VideosHEAT AND TEMPERATURE
FIITJEE|Exercise NUMERICAL BASES QUESTIONS|1 Videos
Similar Questions
Explore conceptually related problems
FIITJEE-GRAVITATION-Solved problem (Subjective)
- There are two fixed heavy masses of magnitude M of high density at a d...
Text Solution
|
- Two satellites of same mass are launched in the same orbit round the e...
Text Solution
|
- A uniform sphere has a mass M and radius R. Find the pressure p inside...
Text Solution
|
- Space junk of mass m leaves its orbit and heads towards on annular di...
Text Solution
|
- With what speed v(0) should a body be projected as shown in the figure...
Text Solution
|
- Three uniform rods, each of mass M and length l, are connected to form...
Text Solution
|
- A planet of mass m moves along an ellipse around the sun so that its m...
Text Solution
|
- An artificial satellite (mass m) of a planet (mass M) revolves in a ci...
Text Solution
|
- A cord of length 64 m is used to connected a 100 kg astronaut to space...
Text Solution
|
- For particles of equal masses M that move along a circle of radius R u...
Text Solution
|