Text Solution
Verified by Experts
Topper's Solved these Questions
ROTATIONAL MECHANICS
FIITJEE|Exercise ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - I|15 VideosROTATIONAL MECHANICS
FIITJEE|Exercise ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - II & III|15 VideosROTATIONAL MECHANICS
FIITJEE|Exercise NUMERICALS BASED QUESTIONS|4 VideosPHYSICS PART2
FIITJEE|Exercise Numerical Based Question Decimal Type|6 VideosSEMICONDUCTOR AND DEVICE
FIITJEE|Exercise SOLVED PROBLEMS Objective: Level-I|20 Videos
Similar Questions
Explore conceptually related problems
FIITJEE-ROTATIONAL MECHANICS-EXERCISE
- Calculate the moment of inertia of a disc of radius R and mass M, abou...
Text Solution
|
- The flywheel of a gasoline engine is required to give up 300 J of kine...
Text Solution
|
- A particle describes uniform circular motion. Find the torque on it ab...
Text Solution
|
- A rectangular plate in the x-y plane is shown in the figure. A force b...
Text Solution
|
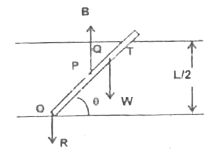
- A uniform rod of length L pivoted at the bottom of a pond of depth L//...
Text Solution
|
- If the particle of mass m is moving with constant velocity v parallel ...
Text Solution
|
- A bullet of mass m collides inelastically at the periphery of a disc o...
Text Solution
|
- What is the moment of the gravitational force of the sun on earth abou...
Text Solution
|
- A small steel sphere of mass m and radius r rolls without slipping on ...
Text Solution
|
- A light rigid rod of length l is constrained to move in a vertical pla...
Text Solution
|
- A sphere of mass M rolls without slipping on rough surface with centre...
Text Solution
|
- As shown in the figure, a rod moves with v = 2 m/sec & rotates with om...
Text Solution
|
- How will you distinguish between a hard boiled egg and a raw egg by s...
Text Solution
|
- Can a body in translatory motion have angular momentum ? Explain.
Text Solution
|