Home
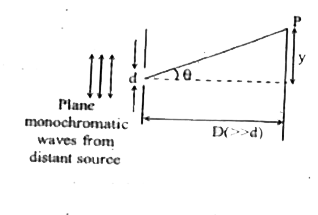
Class 12
PHYSICS
Light of wavelength 6328 Å is incident n...

Light of wavelength `6328 Å` is incident normally on a slit having a width of `0.2 mm`. The distance of the screen from the slit is `0.9 m`. The angular width of the central maximum is

A

2.4 mm

B

1.2 mm

C

0.6 mm

D

4.8 mm

Text Solution

Verified by Experts

The correct Answer is:
B
The angular position of m= 1 minima are given by
`sintheta=pm(lambda)/(d)`
`therefore`   From the adjacent figure, `sintheta=(y)/sqrt((y^(2)+D^(2)))`
If `Deltay` is the distance between the two m = 1 minima, the values of y that correspond to m 1 minima are
`y=pm(1//2)Deltay`
`therefore` `((1)/(2)Deltay)/sqrt(((1)/(2)Deltay)^(2)+D^(2))=(lambda)/(D)`  `rArr` `Deltay=(2D)/sqrt(d^(2)-lambda^(2))`
If `dimplies>lambda` `sqrt(d^(2)-lambda^(2))congd`
`therefore`   `Deltay=(2Dlambda)/(d)=(2xx0.60xx600xx10^(_9))/(0.6xx10^(-3))=12xx10^(-4)=1.2mm`
Promotional Banner

Topper's Solved these Questions

  • ELECTROMAGNETIC WAVE & WAVE OPTICS

    FIITJEE|Exercise ASSIGNMENT PROBLEMS(Subjective: Level-I)|36 Videos

  • ELECTROMAGNETIC WAVE & WAVE OPTICS

    FIITJEE|Exercise ASSIGNMENT PROBLEMS(Subjective: Level-II)|22 Videos

  • ELECTROMAGNETIC WAVE & WAVE OPTICS

    FIITJEE|Exercise SOLVED PROBLEMS Objective: Level-I|10 Videos

  • ELECTROMAGNETIC INDUCTION AND AC CURRENT

    FIITJEE|Exercise Example|15 Videos

  • ELECTROSTANTICS

    FIITJEE|Exercise MATRIX MATCH TYPE|1 Videos

Similar Questions

Explore conceptually related problems

Light of wavelength 6328 Å is incident normally on a slit of width 0.2 mm. Angular width of the central maximum on the screen will be :

Light of wavelength 600 nm is incident normally on a slit of width 0.2 mm. The angular width of central maxima in the diffraction pattern is

Light of wavelength 6328 Å is incident normally on a slit of width 0.2 mm. Calculate the angular width of central maximum on a screen distance 9 m?

Light of wavelength 6328Å is incident normally on slit having a width of 0.2mm The width of the central maximum measured form minimum to minimum of diffraction pattens on a screen 9.0meter away will be about-

Light of wavelength 580 nm is incident on a slit having a width of 0.300 nm The viewing screen is 2.00 m from the slit. Find the positions of the first dark fringe and the width of the central bright fringe.

Monochromatic light with wavelength 420 nm is incident on a slit with width 0.050 mm. The distance from the slit to a screen is 3.5 m. Consider a point on the screen 2.2 cm from the central maximum. Calculate (a) theta for that point, (b) alpha , and (c) the ratio of the intensity at that point to the intensity at the central maximum.

A parallel beam of light of wavelenght 600 nm is incident normally on a slit of width 'd' . If the distance between the slit and screen is 0.8 m and distance of 2nd order maximum from the centre of the screen is 15mm , calculate the width of the slit.

A monochromatic light of wavelength 500 nm is incident normally on a single slit of width 0.2 mm to produce a diffraction pattern. Find the angular width of central maximum obtained on the screen, 1 m away. Estimate the number of fringes obtained in YDSE with fringe width 0.5 mm , which can be accommodated within the region of total angular spread of the central maximum due to a single slit.

A parallel beam of light of wavelength 600 nm is incident normally on a slit of width d. If the distance between the slits and the screen is 0.8 m and the distance of 2^(nd) order maximum from the centre of the screen is 15 mm. The width of the slit is