Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN-NEWTON'S LAWS OF MOTION & FRICTION-EXERCISE (JA)
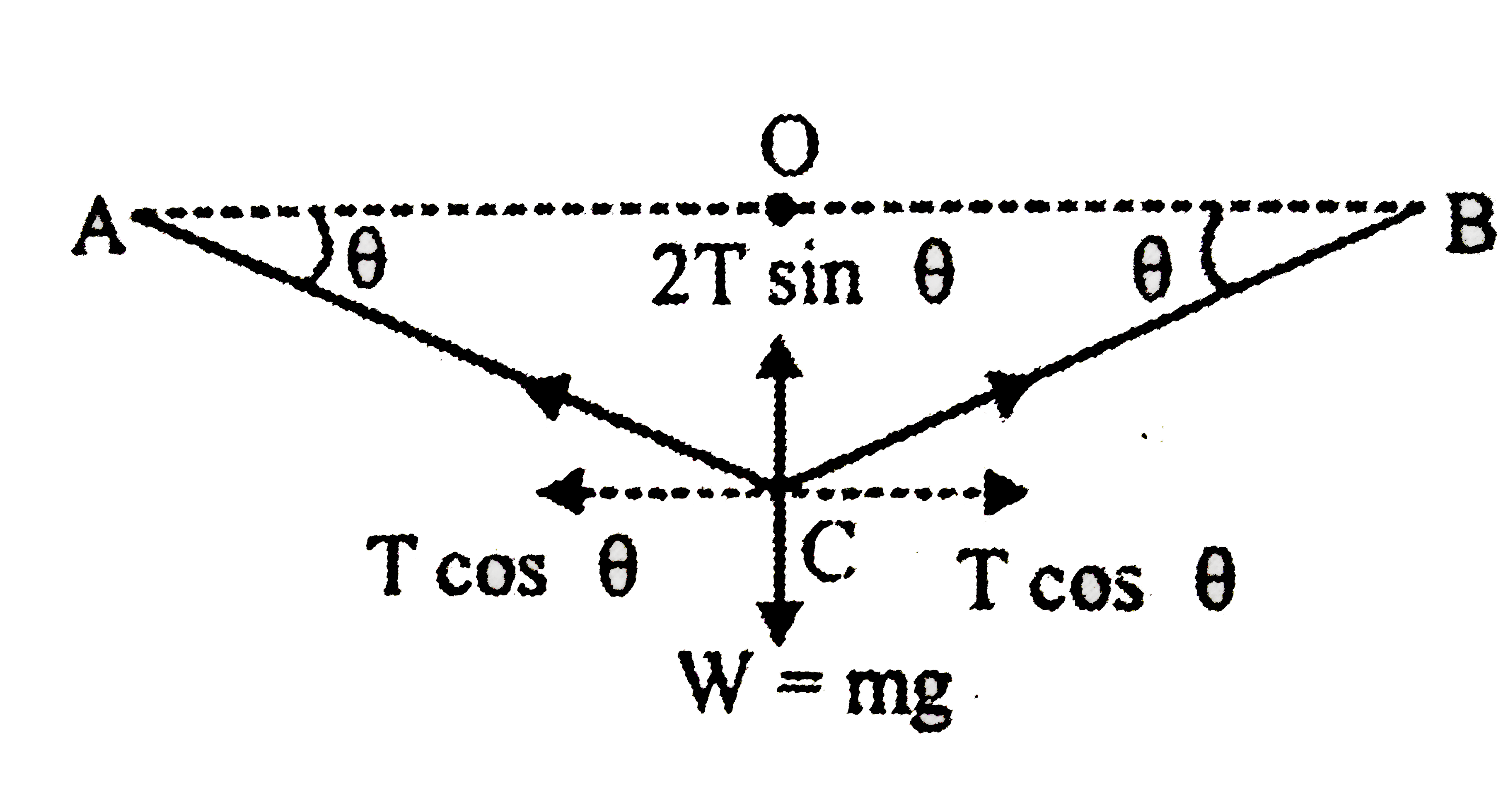
- A bird with mass m parches at the middle of a strectched string Show t...
Text Solution
|
- A piece of wire is bent in the shape of a parabola y=kx^(2) (y-axis ve...
Text Solution
|
- A block of mass m is on an inclined plane of angle theta. The coeffici...
Text Solution
|
- A block is moving on an inclined plane making an angle 45^@ with the h...
Text Solution
|
- A block of mass m1 = 1 kg another mass m2 = 2 kg, are placed together ...
Text Solution
|