A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN-UNIT & DIMENSIONS, BASIC MATHS AND VECTOR -Exercise (J-A)
- Match List I with List II and select the correct answer using the code...
Text Solution
|
- To find the distance d over which a signal can be seen clearly in fogg...
Text Solution
|
- In terms of potential difference V, electric current I, permitivity ep...
Text Solution
|
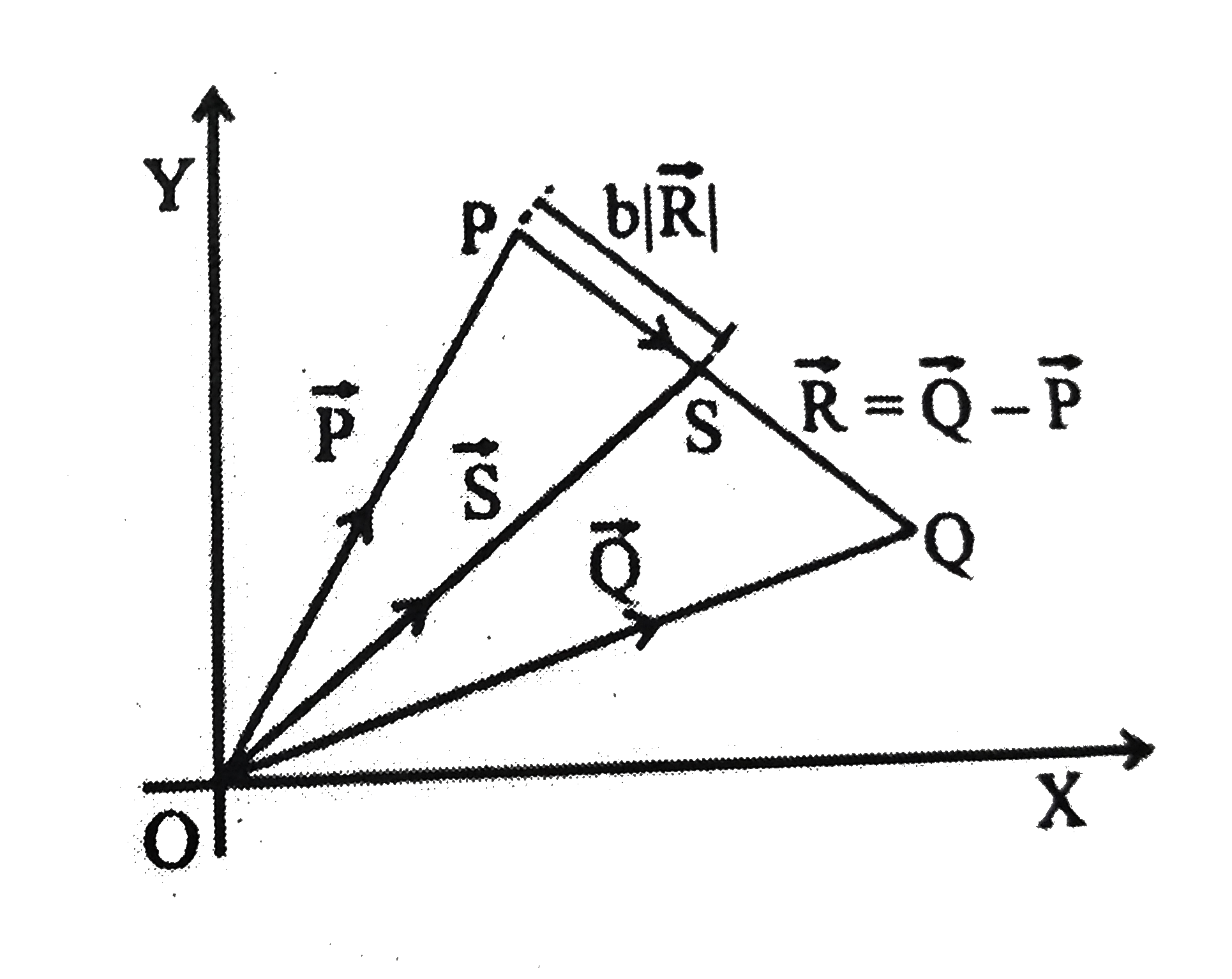
- Three vectors vecP,vecQ " and " vecR are shown in the figure. Let S be...
Text Solution
|
- Two vectors vecA and vecB are defined as vecA=ahati and vecB=a( cos om...
Text Solution
|
- In electromagnetic theory, the electric and magnetic phenomena are rel...
Text Solution
|
- In electromagnetic theory, the electric and magnetic phenomena are rel...
Text Solution
|