A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
MOVING CHARGES AND MAGNETISM
NARAYNA|Exercise EXERCISE - 4|20 VideosMOVING CHARGES AND MAGNETISM
NARAYNA|Exercise EXERCISE - 2(H.W) (FORCE ACTING A MOVING CHARGE IN MAGNETIC FIELD)|14 VideosMAGNETISM AND MATTER
NARAYNA|Exercise EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)|17 VideosNUCLEAR PHYSICS
NARAYNA|Exercise LEVEL-II-(H.W)|9 Videos
Similar Questions
Explore conceptually related problems
NARAYNA-MOVING CHARGES AND MAGNETISM-EXERCISE - 3
- A galvanometer having a coil resistance of 60 Omega shows full scale...
Text Solution
|
- A galvanometer coil has a resistance of 10A and the meter shows full ...
Text Solution
|
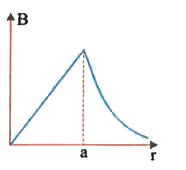
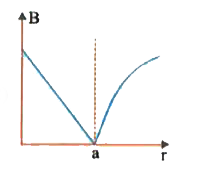
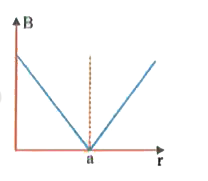
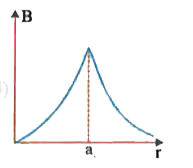
- A long straight wire of a circular cross-section (radius a) carries a ...
Text Solution
|
- The gyromagnetic ratio of an electron of charge e and mass m is equal ...
Text Solution
|
- A beam of cathode rays is subjected to crossed electric (E ) and magn...
Text Solution
|
- A thin ring of radius R metre has charge q coulomb uniformly spread ...
Text Solution
|
- A galvanometer has a a coil resistance 100 ohm and gives a full scale ...
Text Solution
|
- A square current carrying loop is suspended in a unifrom magnetic ...
Text Solution
|
- Charge q is uniformly spread on a thin ring of radius R. The ring rota...
Text Solution
|
- A square loop, carrying a steady current I, is placed in a horizontal ...
Text Solution
|
- A uniform electric field and a uniform magnetic field are acting along...
Text Solution
|
- A current carrying closed loop in the from of a right angle isosel...
Text Solution
|
- An alternating electric field, of frequency v, is applied across the d...
Text Solution
|
- Two similar coils of radius R are lying concentriclaly with their pl...
Text Solution
|
- A current loop in a magnetic field
Text Solution
|
- Two identical long conducting wires AOB and Cod are placed at right an...
Text Solution
|
- A wire carrying current I has the shape as shown in the adjoining ...
Text Solution
|
- A long wire carries a steady curent . It is bent into a circle of one ...
Text Solution
|
- An electron is moving in a circular path under the influence of a tran...
Text Solution
|
- A long staright wire of radius a carries a steady current I. The cure...
Text Solution
|