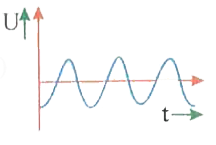
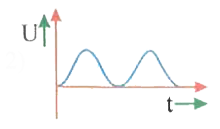
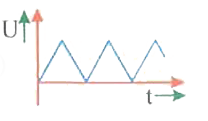A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NARAYNA-OSCILLATIONS-EXERCISE - II (C.W)
- The displacement - time graph of a particle executing SHM is as shown ...
Text Solution
|
- The acceleration of the particle at t = 3 s in the above figure is
Text Solution
|
- The minimum time the particle takes to travel from y = + "1 m to y" = ...
Text Solution
|
- Match the following {:("List - I","List - II"),("(a) acceleration","...
Text Solution
|
- For a particle executing SHM along a straight line (displacement is me...
Text Solution
|
- {:("List - I","List - II"),("(A) x-t graph of simple harmonic oscillat...
Text Solution
|
- The mass and diameter of a planet are twice those of earth. What will ...
Text Solution
|
- The length of a second's pendulum on the surface of the moon, where g ...
Text Solution
|
- The matallic bob of a simple pendulum has the relative density rho. Th...
Text Solution
|
- A pendulum clock is taken 1km inside the earth from mean sea level. Th...
Text Solution
|
- A seconds pendulum is suspended from rof of a vehicle that is moving a...
Text Solution
|
- For a simple pendulum, the graph between T^(2) and L (where T is the t...
Text Solution
|
- In case of a simple pendulum, time period versus length is depicted by
Text Solution
|
- Assuming the earth as an spherical body, for seconds pendulum {:("Co...
Text Solution
|
- {:("List - I","List - II"),("(A) Frequency of seconds pendulum","(E)"A...
Text Solution
|
- For a simple pendulum, a graph is plotted between itskinetic energy (K...
Text Solution
|
- As a body performs SHM its potential energy U. varies with time as ind...
Text Solution
|
- A particle of mass m oscillates with simple harmonic motion between po...
Text Solution
|
- A simple harmonic oscillator (A) Always has maximum KE at the equili...
Text Solution
|
- Which of the following figure represents damped harmonic motion
Text Solution
|