Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
BANSAL-FLUID MECHANICS-EXERCISE # II
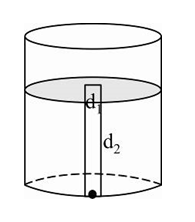
- The tank in fig discharge water at constant rate for all water levels ...
Text Solution
|
- A solid cube, with faces either vertical or horizontal, is floating in...
Text Solution
|
- A glass beaker is placed partially filled with water in a sink it has ...
Text Solution
|
- A wooden cylinder of diameter 4 r, height H and density rho//3 is kept...
Text Solution
|
- A cylindrical rod of length l=2m & density (rho)/(2) floats vertically...
Text Solution
|
- A thin rod of length L and area of cross section S is pivoted at its l...
Text Solution
|
- A hollow cone floats with its axis vertical upto one third of its heig...
Text Solution
|
- In the figure shown, the heavy cylinder (radius R) reasting on a smoot...
Text Solution
|
- A vertical communicating tube contains a liquid of density rho. If it ...
Text Solution
|
- A wooden stick of length L, radius R and density rho has a small metal...
Text Solution
|
- There are two large identical open tanks as shown in figure. In tanks ...
Text Solution
|
- A siphon has a uniform circular base of diameter 8//sqrt(pi) cm with i...
Text Solution
|
- There are two large identical open tanks as shown in figure. In tanks ...
Text Solution
|
- A container of large uniform cross-sectional area A resting on a horiz...
Text Solution
|
- In a cylindrical vessel containing liquid of density rho there are two...
Text Solution
|
- A large open top container of negligible mass and uniform cross-sectio...
Text Solution
|
- A non-viscous liquid of constant density 1000kg//m^3 flows in a stream...
Text Solution
|
- A cube with mass m completely wettable by water floats on the surface ...
Text Solution
|