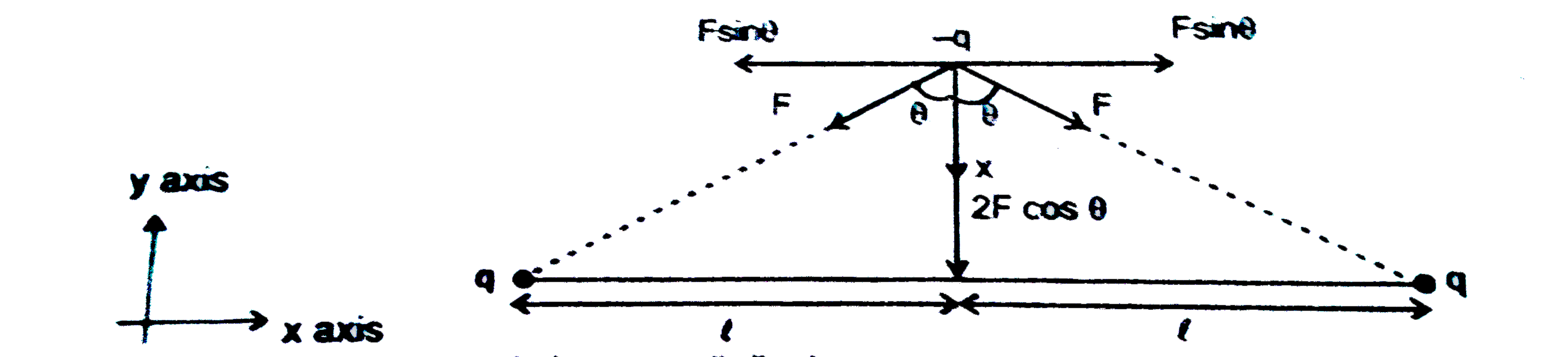
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RESONANCE-ELECTROSTATICS-Problems
- Two equal positive point charges 'Q' are fixed at points B (a, 0) and ...
Text Solution
|
- A particle of mass m and charge q is located midway between two fixed ...
Text Solution
|
- A charges Q is placed at each of the two opposite corners of a square....
Text Solution
|
- An infinitely large non-conducting sheet of thickness t and uniform vo...
Text Solution
|
- Figure shows a uniformly charged thin non-conducting sphere of total c...
Text Solution
|
- Figure shows two concentric spheres of radii R(1) and R(2) (R(2) gt R(...
Text Solution
|
- A solid non conducting sphere of radius R and uniform volume density r...
Text Solution
|
- Three identical spheres, each having a charge q and radius R. are kept...
Text Solution
|
- A uniform electric field of 20 N/C exists in the vertically downward d...
Text Solution
|
- An electric field of 10 N/C exists along the x-axis in space. Calculat...
Text Solution
|
- Some equi-potential surfaces are shown in figure. What can you say abo...
Text Solution
|
- A point charge of charge -q and mass m is released with negligible spe...
Text Solution
|
- Four small point charges (each of equal magnitude q) are placed at fou...
Text Solution
|
- If V=x^(2)y+y^(2)z then find vec(E) at (x, y, z)
Text Solution
|
- Magnitude of electric field only on the x-coordinate as vec(E)=20/x^(2...
Text Solution
|
- If E=2r^(2) then find V(r)
Text Solution
|
- A charge Q is uniformly distributed over a rod of length l. Consider a...
Text Solution
|
- A charge Q is placed at the centre of a cube. Find the flux of the ele...
Text Solution
|
- An isolated conducting sphere of charge Q and radius R is grounded by ...
Text Solution
|
- An isolated conducting sheet of area A and carrying a charge Q is plac...
Text Solution
|