Home
Class 12
MATHS
Consider the following graph of the func...

Consider the following graph of the function y=f(x). Which of the following is//are correct?

`(a) lim_(xto1) f(x)` does not exist.
`(b) lim_(xto2)f(x)` does not exist.
`(c) lim_(xto3) f(x)=3.`
`(d)lim_(xto1.99) f(x)`exists.

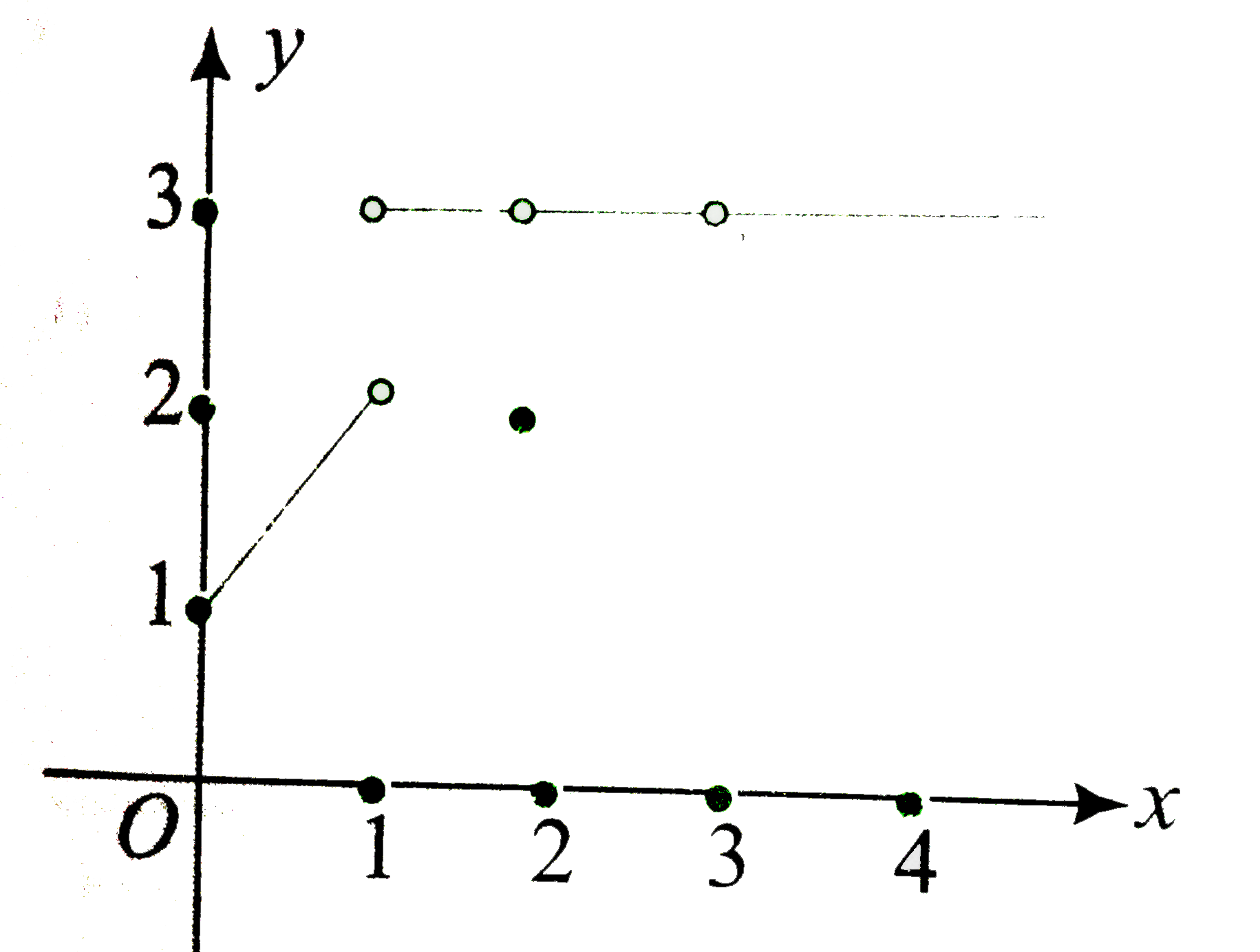
Text Solution

Verified by Experts

The correct Answer is:
(a), ( c ), (d)
`a. underset(xto1^(+))limf(x)=3" and "underset(xto1^(-))limf(x)=2." Thus,"underset(xto1)limf(x)` does not exist.
`b. underset(xto2^(+))limf(x)=underset(xto2^(-))limf(x)=3." Thus,"underset(xto2)limf(x)` exist.
`c. underset(xto3^(+))limf(x)=underset(xto3^(-))limf(x)=3." Thus,"underset(xto3)limf(x)` exist.
`d. underset(xto1.99^(+))limf(x)=underset(xto1.99^(-))limf(x)=3." Thus,"underset(xto1.99)limf(x)` exist.
Promotional Banner

Topper's Solved these Questions

  • LIMITS

    CENGAGE|Exercise Exercise 2.2|7 Videos

  • LIMITS

    CENGAGE|Exercise Exercise 2.3|15 Videos

  • LIMITS

    CENGAGE|Exercise Question Bank|30 Videos

  • JEE 2019

    CENGAGE|Exercise Chapter 10|9 Videos

  • LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORS

    CENGAGE|Exercise DPP 1.2|10 Videos

Similar Questions

Explore conceptually related problems

Consider the following graph of the function y=f(x). Which of the following is/are correct? fig.lim_(x rarr1)f(x) does not exist.lim_(x rarr2)f(x) does not exist.lim_(x rarr3)f(x)=3

Lim f(x) does not exist when

If f(x)=(|x-1|)/(x-1) prove that lim_(x rarr1)f(x) does not exist.

Which of the following statements about the function y=f(x) graphed here are true,an which are false ?( a )lim_(x rarr-1)f(x)=1(b)lim_(x rarr2)f(x) does not exist.

Statement 1: If lim_(xto0){f(x)+(sinx)/x} does not exist then lim_(xto0)f(x) does not exist. Statement 2: lim_(xto0)((e^(1//x)-1)/(e^(1//x)+1)) does not exist.

If f(x)=(|x|)/(x) , then show that lim_(xrarr0) f(x) does not exist.

If f(x)=sgn(x)" and "g(x)=x^(3) ,then prove that lim_(xto0) f(x).g(x) exists though lim_(xto0) f(x) does not exist.

lim_(x rarr c)f(x) does not exist when: (A) f(x)=[[x]]-[2x-1],c=3

If f(x)=(|x-a|)/(x-a) , then show that lim_(xrarra) f(x) does not exist.

Consider the following statements : 1. If lim_(xtoa) f(x) and lim_(xtoa) g(x) both exist, then lim_(xtoa) {f(x)g(x)} exists. 2. If lim_(xtoa) {f(x)g(x)} exists, then both lim_(xtoa) f(x) and lim_(xtoa) g(x) must exist. Which of the above statements is /are correct?