Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN-KINEMATICS-2D-Exercise (S-2)
- A particle travels so that its acceleration is given by vec(a)=5 cos t...
Text Solution
|
- A man can throw a stone with initial speed of 10 m//s. Find the maximu...
Text Solution
|
- Two inclined planes OA and OB having inclination (with horizontal) 30^...
Text Solution
|
- A projectile si thrown with velocity of 50m//s towards an inclined pla...
Text Solution
|
- A small squirrel jumps from pole 1 to pole 2 in horizontal direction. ...
Text Solution
|
- Two particles starts simultaneously from a point O and move along line...
Text Solution
|
- Two guns situated at the top of a hill of height 10 m fire one shot ea...
Text Solution
|
- A hunter is riding an elephant of height 4 m moving in straight line w...
Text Solution
|
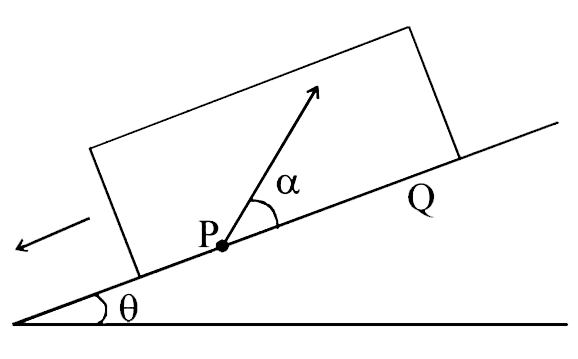
- A large , heavy box is sliding without friction down a smooth plane o...
Text Solution
|
- A particle is projected from ground towards a vertical wall 80 m away ...
Text Solution
|
- You are standing on the Bridge watching the boats in the river. You se...
Text Solution
|
- Two swimmers start a race. One who reaches the point C first on the ot...
Text Solution
|
- A swimmer starts to swim from point a to cross a river. He wants to re...
Text Solution
|
- Hailstones falling vertically with speed of 10 m/s hit with respect to...
Text Solution
|
- A motor boat set out at 11a.m. from a position -6hati-2hatj relative t...
Text Solution
|