Home
Class 12
MATHS
Prove that cos (tan^(-1) (sin (cot^(-1) ...

Prove that `cos (tan^(-1) (sin (cot^(-1) x))) = sqrt((x^(2) + 1)/(x^(2) + 2))`

Text Solution

Verified by Experts

`E = cos (tan^(-1) (sin (cot^(-1) x)))`
Let `cot^(-1) x = theta`

`:. E = cos [tan^(-1) (sin (sin^(-1).(1)/(sqrt(1 + x^(2))))] " if " x gt 0`
or `E = cos [tan^(-1) (sin (pi - sin^(-1).(1)/(sqrt(1 + x^(2)))))] " if " x lt 0`
In each case, `E = cos [tan^(-1) (1)/(sqrt(1 + x^(2)))]`
`:. E = cos [cos^(-1) sqrt((1 + x^(2))/(2 + x^(2)))]`
`= sqrt((x^(2) + 1)/(x^(2) + 2))`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • INVERSE TRIGONOMETRIC FUNCTIONS

    CENGAGE|Exercise Exercise 7.1|12 Videos

  • INVERSE TRIGONOMETRIC FUNCTIONS

    CENGAGE|Exercise Exercise 7.2|6 Videos

  • INTRODUCTION TO VECTORS

    CENGAGE|Exercise JEE Previous Year|20 Videos

  • JEE 2019

    CENGAGE|Exercise Chapter 10|9 Videos

Similar Questions

Explore conceptually related problems

Prove that cos [tan^(-1){(sin(cot^(-1)x}] =((x^(2)+1)/(x^(2)+2)) ^(1/2)

Prove that cos[tan^(-1){sin(cos^(-1)x)}]=(1)/(sqrt(2-x^(2)))

Prove that : sin cot^(-1) tan cos^(-1) x=x

Prove the following: cos{tan^(-1){sin(cot^(-1)x)}}=sqrt((1+x^(2))/(2+x^(2)))

Prove that tan^(-1) x + cot^(-1) (x+1) = tan ^(-1) (x^(2) + x+1) .

Prove that : tan^(-1) x + cot^(-1) (1+x) = tan^(-1) (1+x+x^2)

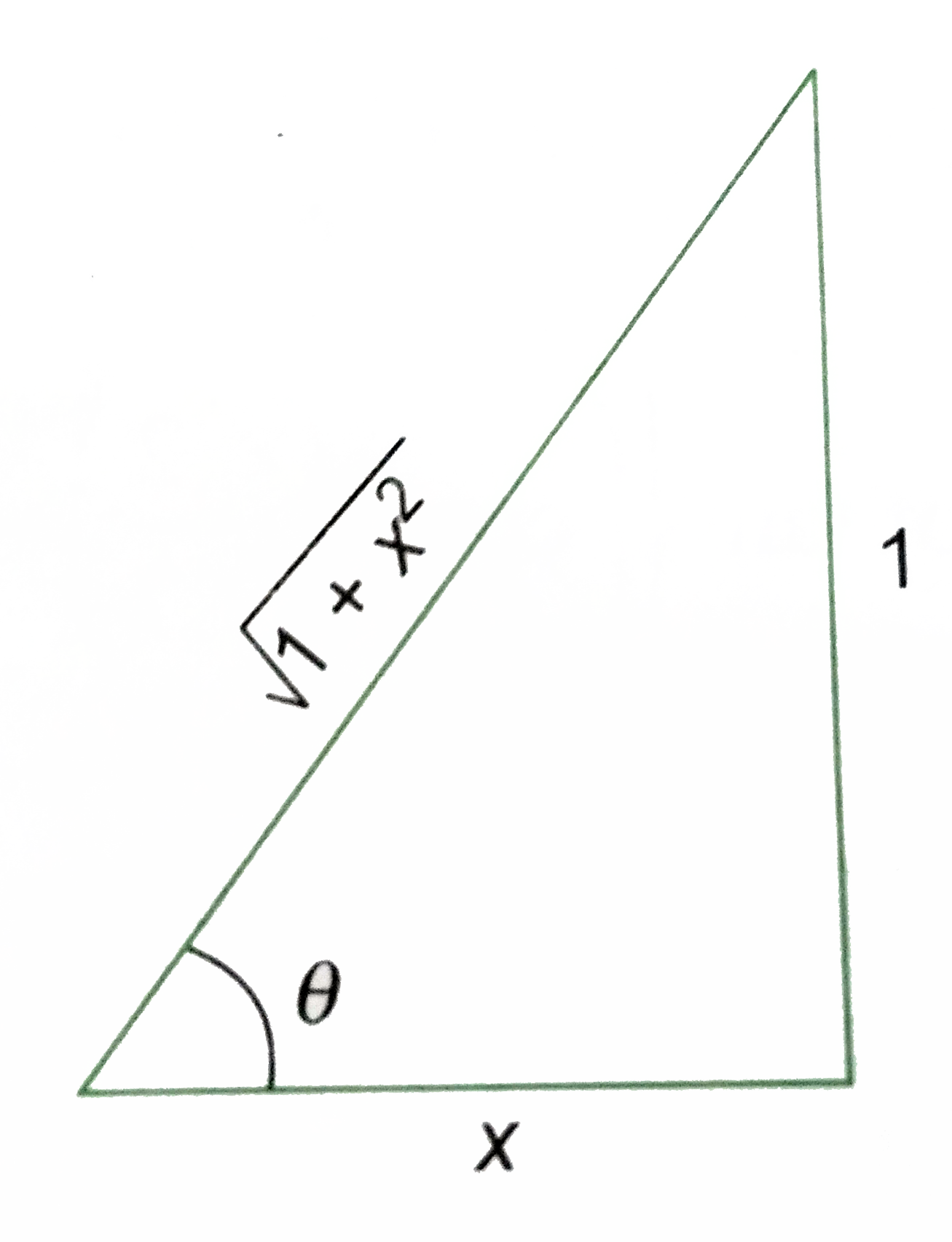
Prove that: sin[cot^(-1){cos(tan^(-1)x)}]=sqrt((x^(2)+1)/(x^(2)+2))cos[tan^(^^)(-1){sin(cot^(-1)x)}]=sqrt((x^(2)+1)/(x^(2)+2))

Prove that sin [2 tan^(-1) {sqrt((1 -x)/(1 + x))}] = sqrt(1 - x^(2))

Prove that : 2 tan^(-1) (cosec tan^(-1) x - tan cot^(-1) x) = tan^(-1) x

Prove that sin^(-1)x=cos^(-1) sqrt(1-x^2)

Home
Profile