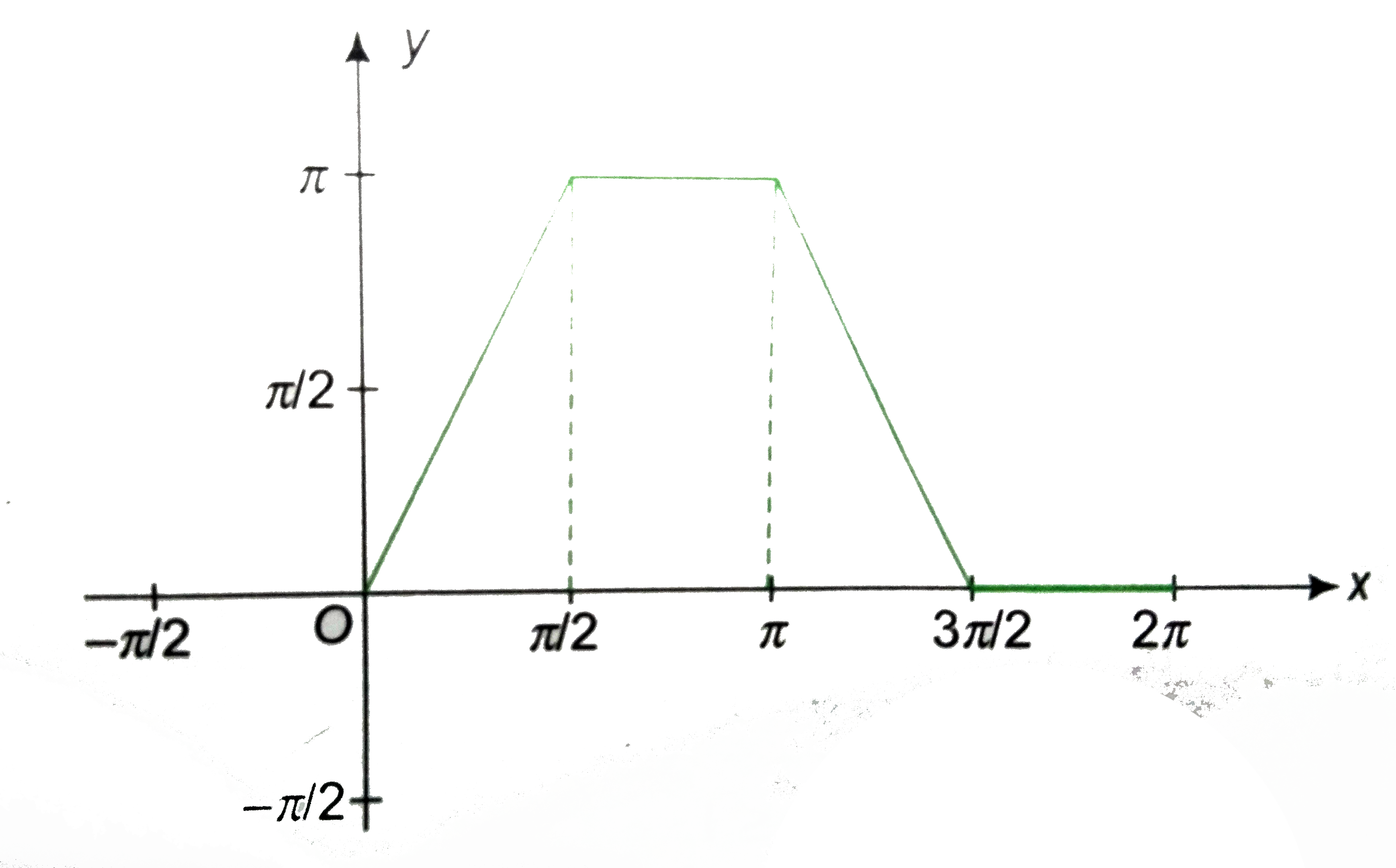
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
INVERSE TRIGONOMETRIC FUNCTIONS
CENGAGE|Exercise Exercise 7.3|12 VideosINVERSE TRIGONOMETRIC FUNCTIONS
CENGAGE|Exercise Exercise 7.4|12 VideosINVERSE TRIGONOMETRIC FUNCTIONS
CENGAGE|Exercise Exercise 7.1|12 VideosINTRODUCTION TO VECTORS
CENGAGE|Exercise JEE Previous Year|20 VideosJEE 2019
CENGAGE|Exercise Chapter 10|9 Videos
Similar Questions
Explore conceptually related problems
CENGAGE-INVERSE TRIGONOMETRIC FUNCTIONS-Exercise 7.2
- Find the following values : (a) tan^(1) tan.(13pi)/(5) (b) sec^(-1) ...
Text Solution
|
- If f(x) = sin^(-1) (sin ("log"(2) x)), then find the value of f(300)
Text Solution
|
- find the maximum value of f(x) = (sin^(-1) (sin x))^(2) - sin^(-1) (si...
Text Solution
|
- solve sin^(-1) (sin 5) gt x^(2) - 4x
Text Solution
|
- Consider function f(x) = sin^(-1) (sin x) + cos^(-1) (cos x), x in [0,...
Text Solution
|
- Find the values of x in [0,2pi] for which function f(x) = tan^(-1) (ta...
Text Solution
|