Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-COORDINATE SYSYEM -Exercise 1.3
- If point P(3,2) divides the line segment AB internally in the ratio of...
Text Solution
|
- If the point (x ,-1),(3, y),(-2,3),a n d(-3,-2) taken in order are ...
Text Solution
|
- If the midpoints of the sides of a triangle are (2,1),(-1,-3),a n d(4,...
Text Solution
|
- The line joining A(bcosalphabsinalpha) and B(acosbeta,asinbeta) is pro...
Text Solution
|
- If the middle points of the sides of a triangle are (-2,3),(4,-3),a...
Text Solution
|
- Find the incentre of the triangle with vertices (1, sqrt3), (0, 0) and...
Text Solution
|
- If (1,4) is the centroid of a triangle and the coordinates of its a...
Text Solution
|
- The vertices of a triangle are A(x1,x1tantheta1),B(x2, x2tantheta2), a...
Text Solution
|
- If (xi,yi),i=1,2,3 are the vertices of an equilateral triangle such th...
Text Solution
|
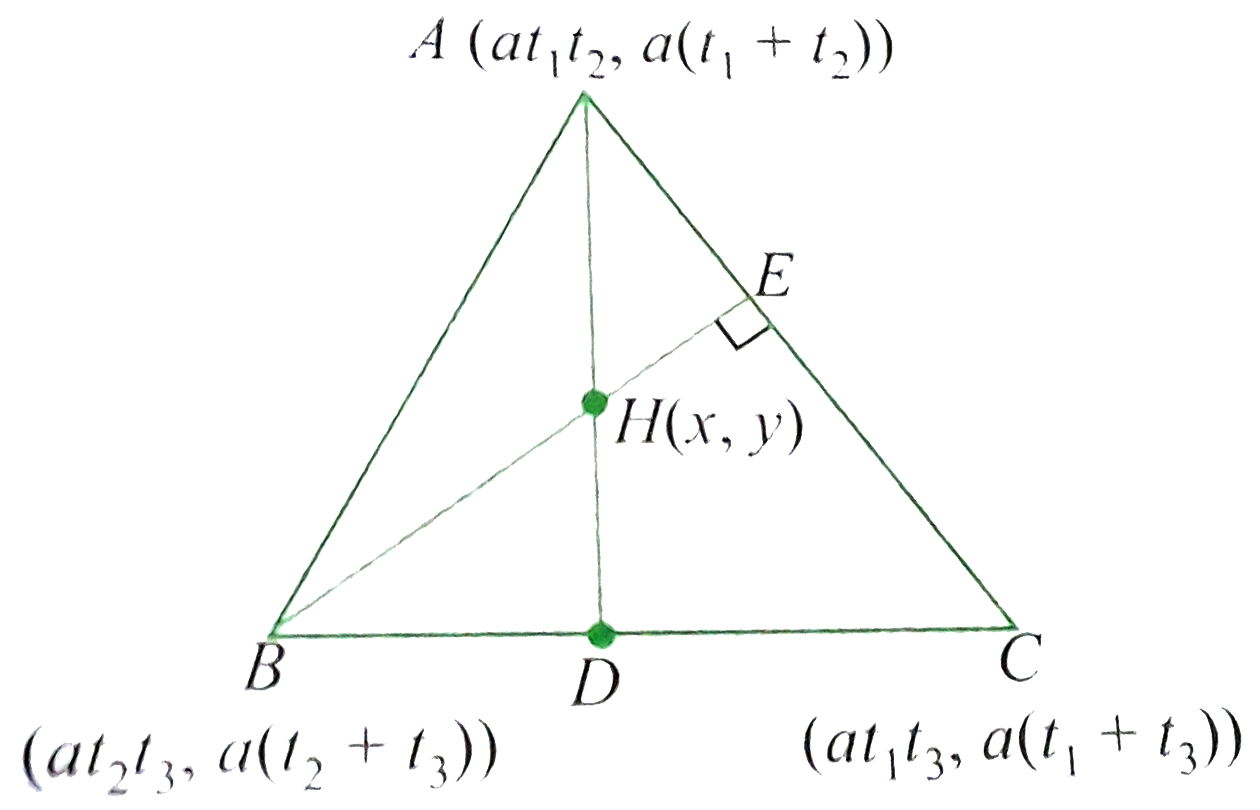
- The vertices of a triangle are [a t1t2,a(t1 +t2)], [a t2t3,a(t2 +t3)],...
Text Solution
|