Home
Class 9
MATHS
In Fig. 10.37, /P Q R\ =\ 100^@, where ...

In Fig. 10.37, `/_P Q R\ =\ 100^@`, where P, Q and R are points on a circle with centre O. Find `/_O P Rdot`

Text Solution

Verified by Experts

Since all points `P, Q, R, S` lie on the circle, `PQRS` becomes a cyclic quadrilateral.
We know that the sum of either pair of opposite angles of a cyclic quadrilateral is `180^@`
Therefore,`anglePQR + anglePSR = 180^@`
`100^@ + anglePSR = 180^@`
`anglePSR = 180^@ - 100^@ = 80^@`
We know that the angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle
Therefore,`anglePOR = 2anglePSR`
= `2 × 80^@`
= `160^@`
Consider the `triangleOPR`. It is an isosceles triangle as `OP = OR` = Radius of the circle.
Thus, `angleOPR = angleORP`
Sum of all angles in a triangle is `180^@`
Therefore, `angleOPR + anglePOR + angleORP = 180^@`
`angleOPR + 160^@ + angleOPR = 180^@`
`2angleOPR = 180^@ - 160^@`
`angleOPR = 10^@`
Promotional Banner

Topper's Solved these Questions

  • CIRCLES

    NCERT|Exercise EXERCISE 10.2|2 Videos

  • CIRCLES

    NCERT|Exercise Exercise 10.4|6 Videos

  • AREAS OF PARALLELOGRAMS AND TRIANGLES

    NCERT|Exercise EXERCISE 9.1|1 Videos

  • CONSTRUCTIONS

    NCERT|Exercise EXERCISE 11.2|5 Videos

Similar Questions

Explore conceptually related problems

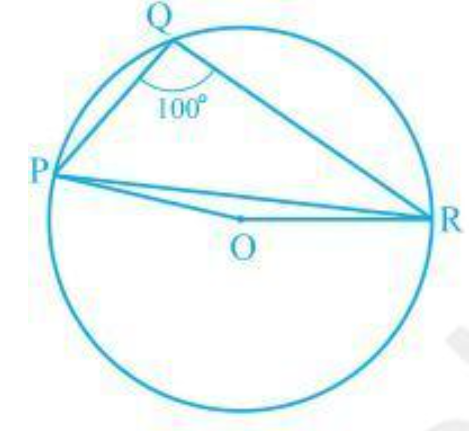
In Figure,/_PQR=100^(@), where P,Q and R are points on a circle with centre. O.Find /_OPR

In the given figure, angle PQR = 100^(@), where P, 9 and R are points on a circle with centre O. Find angle OPR.

In the given figure angle PQR = 100^(@) , where P, Q, R are points on a chords with centre O. Find the measure of angle OPR .

In Fig. 10.95, P Q and P R are tangents drawn from P to a circle with centre O . If /_O P Q=35o , then (FIGURE) a=30o, b=60o (b) a=35o, b=55o (c) a=40o, b=50o (d) a=45o, b=45o

In Fig. 10.88, A P B is a tangent to a circle with centre O at point P . If /_Q P B=50o , then the measure of /_P O Q is (FIGURE) 100o (b) 120o (c) 140o (d) 150o

In Fig. 6.15, /_P Q R=/_P R Q , then prove that /_P Q S=/_P R T .

In Fig. 6.39, sides QP and RQ of DeltaP Q R are produced to point S and T respectively. If /_S P R=135^@ and /_P Q T=110^@ , find /_P R Q.

The sides AB,BC and AC of a triangle ABC touch a circle with centre O and radius r at P Q,and R respectively.

In Fig.77, find out /_P X R , if P Q R Sdot