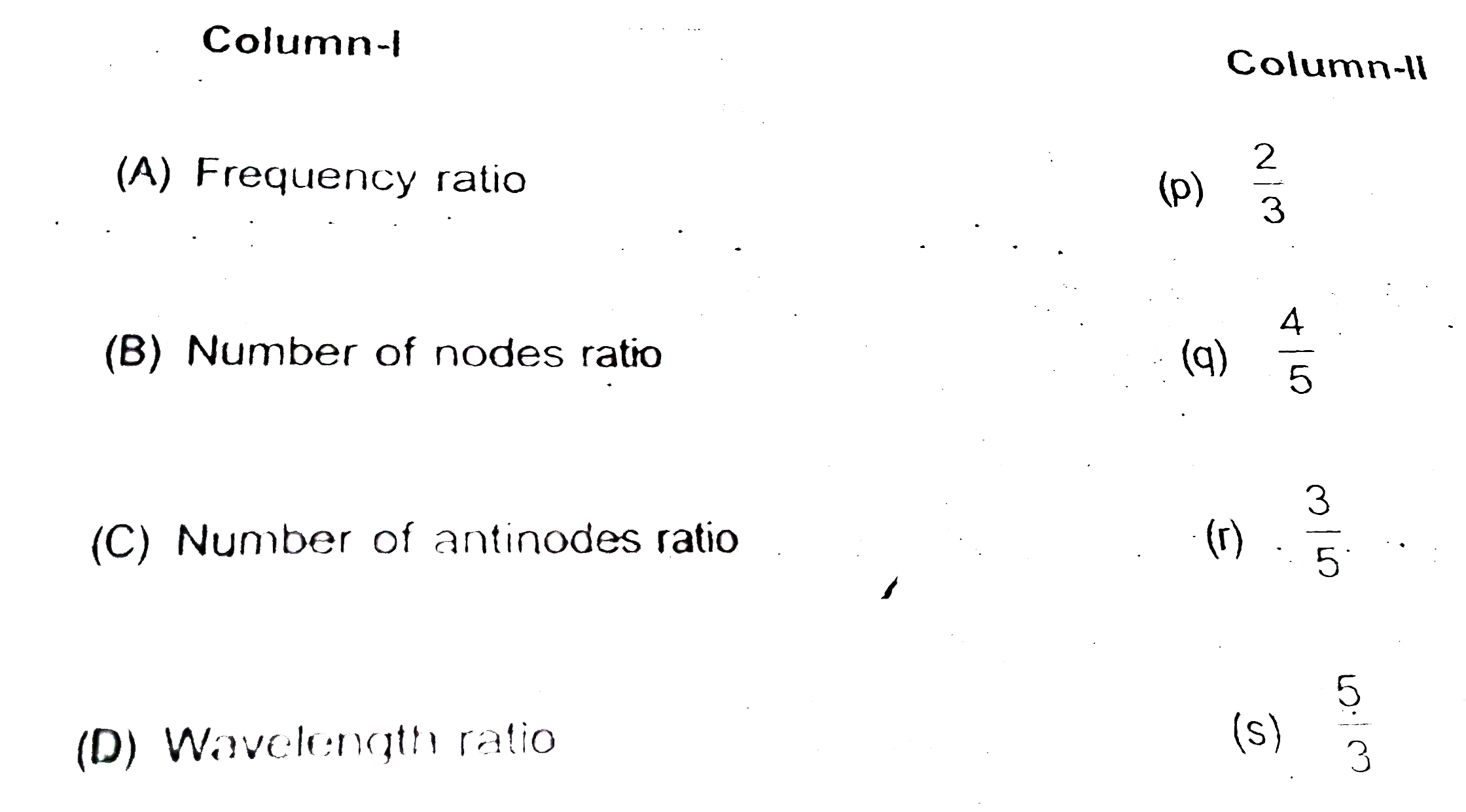A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NARAYNA-WAVES-Exercise-II (C.W)
- Figure shows the shape of a string , the pairs of points which are in ...
Text Solution
|
- Transverse waves are produced in a long string by attaching its free e...
Text Solution
|
- y-x graph of a transverse wave at a given instant is shown in figure. ...
Text Solution
|
- Shows a snapshot of a travelling wave taken at t=0.3s. The wavelength...
Text Solution
|
- A uniform rope having some mass hinges vertically from a rigid support...
Text Solution
|
- Two pulse in a stretched string whose centers are initially 8cm apart ...
Text Solution
|
- The graph between distance between source and observer and apparent fr...
Text Solution
|
- The distribution of the sound intensity of the whistle as observed by ...
Text Solution
|
- The correct match is
Text Solution
|
- Transverse waves are produced in a stretched wire. Both ends of the st...
Text Solution
|
- A wave travels from a denser medium to rarer medium, then match the fo...
Text Solution
|
- A tuning fork 'P' of frequency 280Hz produces 6 beats/s with unknown t...
Text Solution
|
- A string of length 1 is stretched along the x-axis and is rigidly clam...
Text Solution
|
- The tension in a stretched string fixed at both ends is changed by 2%,...
Text Solution
|
- The equation of the standing wave in a string clamped at both ends, vi...
Text Solution
|