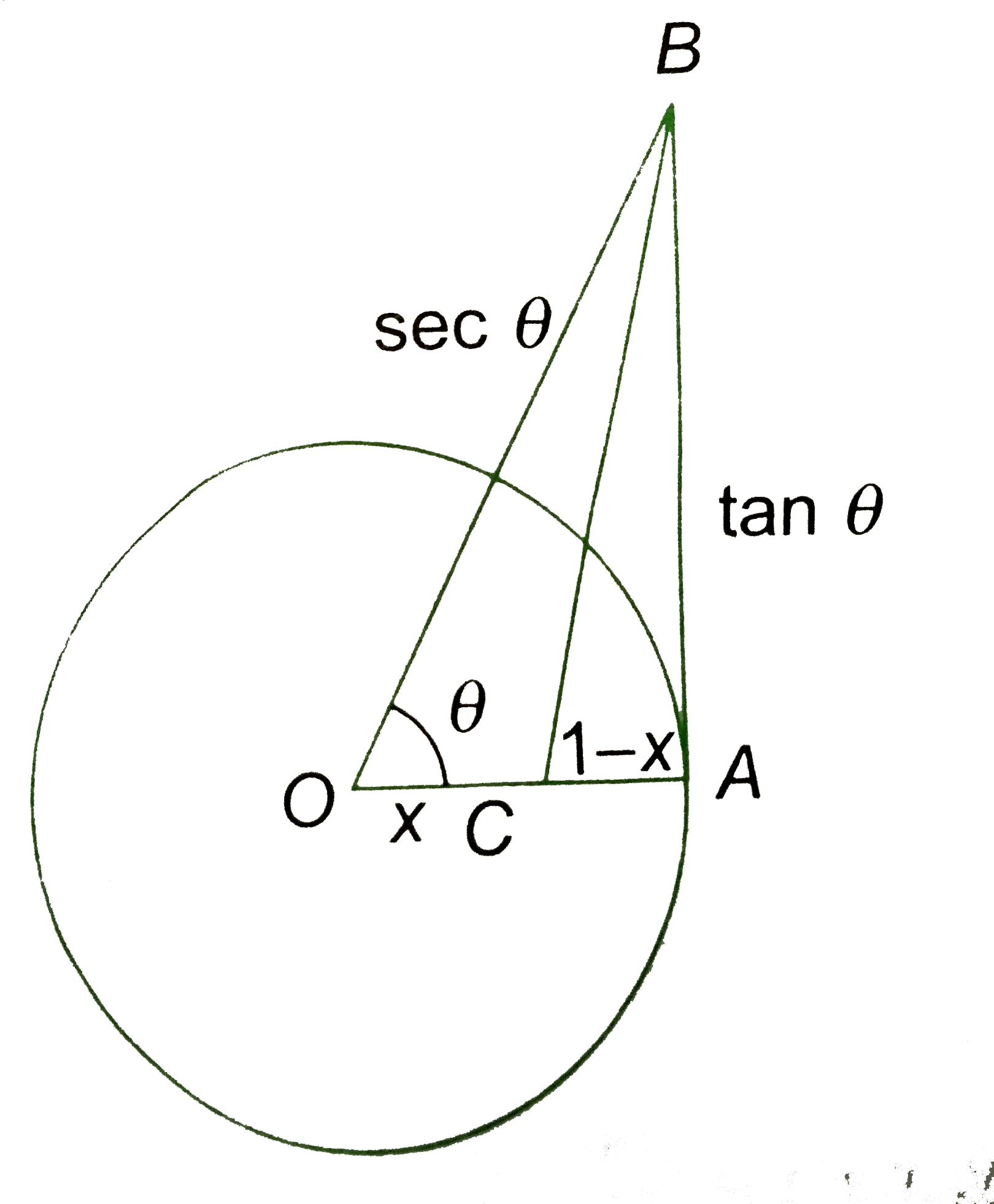A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
TRIGONOMETRIC FUNCTIONS
CENGAGE|Exercise Exercise (Comprehension)|11 VideosTRIGONOMETRIC FUNCTIONS
CENGAGE|Exercise Exercise (Matrix)|3 VideosTRIGONOMETRIC FUNCTIONS
CENGAGE|Exercise Exercise (Single)|57 VideosTRIGONOMETRIC EQUATIONS
CENGAGE|Exercise Archives (Matrix Match Type)|1 VideosTRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
CENGAGE|Exercise Matrix Match Type|1 Videos
Similar Questions
Explore conceptually related problems
CENGAGE-TRIGONOMETRIC FUNCTIONS -Exercise (Multiple)
- If 0 le theta lepi and 8 1^(sin^2theta)+8 1^(cos^2theta)=30 is
Text Solution
|
- Suppose ABCS (in order) is a quadrilateral inscribed in a circle. Whic...
Text Solution
|
- Which of the following is/are correct ?
Text Solution
|
- If 3tanA+4=0, then the value of 2cotA-5cosA+sinA is equal to
Text Solution
|
- A circle centred at 'O' has radius 1 and contains the point A. Segment...
Text Solution
|
- (a+2)sinalpha(2a-1)cosalpha=(2a+1)if tanalpha is
Text Solution
|
- Leg f(x)=log((log)(1//3)((log)(1/3)((log)7(sinx+a))) be defined for ev...
Text Solution
|
- If bgt1, sintgt0,costgt0andlogb(sint)=x," then "logb(cost) is equal to
Text Solution
|
- Which of the following is possible in DeltaABC?
Text Solution
|
- If 2sec^2 alpha- sec^4 alpha-2 cosec^2 alpha+cosec^4 alpha=15/4 then t...
Text Solution
|
- If cottheta+tantheta=xand sectheta-costheta=y, then
Text Solution
|
- If x=secphi -tanphi and y="cosec" phi+cotphi, then show that xy+x-y+1...
Text Solution
|
- The value of f(alpha)=sqrt(cos e c^2alpha-2cotalpha)+sqrt(cos e c^2alp...
Text Solution
|
- If (y+3)/(2y+5) = sin^2x + 2 cosx+1, then the value of y lies in
Text Solution
|
- If cosalpha=1/2(x+1/x) cosbeta=1/2(y+1/y) then cos(alpha-beta) is equa...
Text Solution
|
- Four numbers n1,n2,n3andn4 are given as n1=sin15^@-cos15^@,n2=cos93^@+...
Text Solution
|
- For 0ltphiltpi//2," if" x=sum(n=0)^(oo) cos^(2n)phi,y=sum(n=0)^(oo) si...
Text Solution
|