अन्योन्य प्रेरण- एक कुण्डली में धारा परिवर्तन के कारण इसकी कुण्डली में वि.वा. बल प्रेरित होने की घटना को अन्योन्य प्रेरण कहते है।
प्रथम परिपथ प्राथमिक तथा द्वितीयक - परिपथ द्वितीयक परिपथ कहलाता है।
`E_(2)=-M (dI_(1))/(dt)`
अन्योन्य प्रेरण गुणाक यदि प्राथमिक कुण्डली A में धारा `I_(1)` प्रवाहित होती है तब उसके कारण उत्पन्न चुम्बकीय क्षेत्र इस धारा के समानुपाती होता है। चूकि द्वितीयक कण्डली से पार होने वाला फ्लक्स `(phi B)_(2)` इस चुम्बकीय क्षेत्र के समानुपाती होता है। अतः
`therefore (phi B)_(2) alpha I_(1)`
`(phi B)_(2)=MI_(1) ........(1)`
यहाँ पर M को अन्योन्य प्रेरण गुणांक कहते हैं। यदि प्राथमिक कुण्डली में धारा I परिवर्तित हो रही हो, तो द्वितीयक कुण्डली से पार होने वाले फ्लक्स `(phi B)_(2)` में भी परिवर्तन होता है जिससे द्वितीयक कुण्डली में प्रेरित वि.वा. बल उत्पन्न होता है।
प्रेरित वि.वा. बल `E_(2)=- (d(phi B)_(2))/(dt)`
`E_(2)=-d/ (dt) (MI_(1))`
(समी. (1) में मान रखने पर)
`E_(2)=-M (dI_(1))/(dt)` ...(2)
समीकरण (2) से, `M=-(E_(1))/((dI_(1))/(dt))` ......(3)
"द्वितीयक कुण्डली में प्रेरित वि.या. बल एवं प्राथमिक कुण्डली धारा परिरवतनं की दर के अनुपात को अन्योन्य प्रेरण गुणांक कहते हैं।"
समीकरण (1) से,
`M=((phi B)_(2))/(I_(1))`
इसके अनुसार "द्वितीयक कुण्डली से पार होने वाली कुल फ्लक्स एवं प्राथमिक कुण्डली में प्रवाहित धारा के अनुपात को अन्योन्य प्रेरण गुणांक कहते हैं।"
दो लम्बी समाक्षीय परिनालिकाओं का अन्योन्य
प्रेरकत्व - चित्र में दो समाक्षीय परिनालिकाएं `S_1" व "S_2` प्रदर्शित हैं। इनमें फेरों की संख्या क्रमशः `N_1" व "N_2` है।
और परिनालिका `S_2` परिनालिका `S_1` को पूर्णतः घेरै हुए है- दोनों की ला्बाई है तथा प्रत्येक का अनुप्रस्थ परिच्छेद क्षेत्रफल A है।
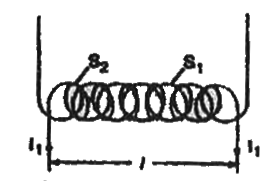
`S_1` परिनालिका की एकांक लंबाई में फेरों की सख्या
`n_(1)=N_(1)/1 ......(1)`
और S, परिनालिका का एकांक लम्बाई में फेरों की संख्या
`n_(2)=N_(2)/1 ....(2)`
यदि परिनालिका `S_1" में धारा "I_2` बहने से उसके अन्दर उत्पन्न चुम्बकीय क्षेत्र `B_1` हो, तो
`B_(1)=mu_(0) n_(1)I_(1)`
`mu_(0) N_(1)/1 .I_(1) .....(3)`
`S_(2)` के प्रत्येक फेरे के साथ सम्बुद्ध चुम्बकीय फलस्क `=B,A`
अंत: `S_(2)` के प्रत्येक फेरे के साथ सम्बुद्ध चुम्बकीय फलस्क
`phi_(2)=N_(2). (B_(1)A)`
`N_(2).mu_(0) N_(1)/1. I_(1) A`
या `phi_(2)=(mu_(0) N_(1)N_(2) A.I_(1))/(1) ........(4)`
परन्तु अन्यान्य प्रेरण से, `phi_(2)=M_(12)I_(1) .......(5)`
समीकरण (4) व् (5) की तुलना करने पर
`M_(12)I_(1)=(mu_(0) N_(1)N_(2) A.I_(1))/(1)`
`therefore M_(12)=(mu_(0) N_(1)N_(2)A)/(1)`
