सयुंक्त सूक्ष्मदर्शी - यह दो लेंसों से बना एक ऐसा प्रकाशिक यंत्र है जिससे समीप की सूक्ष्म वस्तु का आवर्धित प्रतिबिम्ब बनता है इस प्रतिबिम्ब बनता है इस प्रतिबिम्ब द्वारा प्रेक्षक की आँख पर बना दर्शन कोण काफी बड़ा होता है फलतः आँख को वस्तु बड़ी दिखाई देती है।
रचना - इसमें धातु की बनी एक लम्बी तथा बेलनाकार नाली होती है जिसके एक सिरे पर कम फोकस दूरी तथा छोटे द्वारक का अवर्णक उत्तल लेंस O लगा रहता है जैसा चित्र में दिखाया गया है इसको वस्तु की ओर करके रखा जाता है जिसे हम अभिदृश्यक लेंस कहते है अभिदृश्यक लेंस का द्वारक छोटा लेने का कारण यह है कि यह निकट की सूक्ष्म वस्तुओं को देखने के काम आता है।
यदि अभिदृश्यक का द्वारक बड़े द्वारक में फैलेगा ओर वस्तु कम चमकीली दिखाई देगी। इसके विपरीत द्वारक छोटा लेने से चलने वाला प्रकाश छोटे द्वारक में फैलेगा जिससे प्रतिबिम्ब चमकीला प्राप्त होने से वस्तु चमकीली दिखाई देगी।
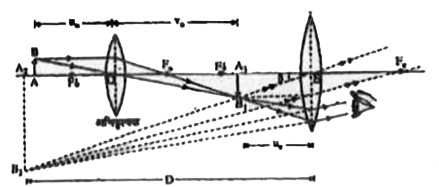
सूक्ष्मदर्शी की बेलनाकार नाली से दूसरे सिरे पर एक अन्य छोटी नाली लगी होती है जिसका दन्तुर दण्ड वक्र व्यवस्था द्वारा बेलनाकार नली के अंदर आगे - पीछे खिसकाया जा सकता है। इस छोटी नली के बाहर वाले सिरे पर अभिदृश्यक की तुलना में बड़ी फोकस दूरी तथा बड़े द्वारक का एक अन्य अवर्णक उत्तल लेंस E लगा रहता है इस लेंस को आँख की ओर करके रखा जाता है अतः इसे नेत्रिका कहते है इसके फोकस पर छोटी नली में क्रॉस - तार लगे रहते है।
कार्यप्रणाली - चित्र में दिखाया गया है वस्तु AB को अभिदृश्यक लेंस के सामने लेंस की फोकस दूरी से कुछ आगे की ओर रखते है वस्तु से निकलने वाली किरणें इस लेंस से अपवर्तित होकर वस्तु का `A_(1)B_(1)` वास्तविक, उलटा व आवर्धित प्रतिबिम्ब बनाती है यह प्रतिबिम्ब अभिनेत्र लेंस के लिए वस्तु का कार्य करता है
अब हम नेत्र लेंस को इस प्रकार समंजित करते है कि प्रतिबिम्ब `A_(1)B_(1)` नेत्र लेंस के फोकस एवं प्रकाश केंद्र के बीच में बने। नेत्र लेंस के फोकस एवं प्रकाश केंद्र के बीच में बने। नेत्र लेंस वास्तविक रूप से सरल सूक्ष्मदर्शी के रूप में कार्य करके अब इसका आवर्धित आभासी प्रतिबिम्ब `A_(2)B_(2)` बनता है। नेत्र लेंस की स्थिति ऐसे समंजित करते है जिससे `A_(2)B_(2)` नेत्र से D दूरी पर बने अंतिम प्रतिबिम्ब `A_(2)B_(2)` प्रतिबिम्ब `A_(1)B_(1)` के सापेक्ष सीधा परन्तु वस्तु AB के सापेक्ष उल्टा होता है।
आवर्धन क्षमता - संयुक्त सूक्ष्मदर्शी की आवर्धन क्षमता इसके द्वारा बने अन्तिम प्रतिबिम्ब द्वारा आँख पर बने दर्शन कोण तथा वस्तु द्वारा आँख पर बने दर्शन कोण (जबकि वस्तु स्पष्ट दृष्टि की न्यूनतम दूरी पर हो तथा बिना यंत्र के सीधी देखी जा रही हो के अनुपात के बराबर होती है
अतः आवर्धन क्षमता अर्थात कोणीय आवर्धन
अन्तिम क्षमता अर्थात कोणीय आवर्धन
`m =("बना कोण")/("वस्तु द्वारा आँख पर बना कोण")` माना अन्तिम प्रतिबिम्ब `A_(2)B_(2)` नेत्रिका E पर `beta` कोण बनाता है चूंकि आँख के समीप है अतः `beta` को ही `A_(2)B_(2)` द्वारा आँख पर बना कोण मान सकते है (चित्र I ) यदि वस्तु AB आंख से स्पष्ट दृष्टि की न्यूनतम दूरी D पर रखी होने पर आंख द्वारा रखे जाने पर आँख पर `alpha` कोण बनाती है (चित्र II ) तो सूक्ष्मदर्शी की आवर्धन क्षमता
`m=(beta)/(alpha)` . . . . .(1)
चूंकि वस्तु छोटी है अतः कोण `alpha,beta` भी बहुत छोटे होंगे अतः इनके स्थान पर इनकी स्पर्श ज्या (tan) ले सकते है।
`:.alpha=tanalpha ` तथा `beta=tan beta`
`:. m=(tan beta)/(tan alpha)` . . . (2)
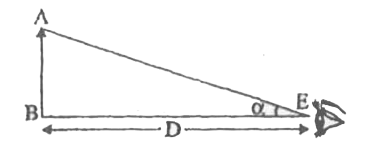
परन्तु (चित्र II ) समकोण त्रिभुज ABE से,
`tan alpha=(AB)/(D)` . . .(3)
तथा (चित्र I ) में समकोण त्रिभुज `B_(1)A_(1)E` से ,
`tan beta =(A_(1)B_(1))/(EA_(1))` . . . . (4)
(2) में समीकरण (3) तथा (4) का मान रखने पर
`m=(A_(1)B_(1)//EA_(1))/(AB//D)=(A_(1)B_(1))/(AB)((D)/(EA_(1)))` . . .(5)
यदि वस्तु AB तथा प्रतिबिम्ब `A_(1)B_(1)` की अभिदृश्यक O से दूरियां क्रमशः `mu_(0)` तथा `v_(0)` हों तो इनके उचित चिन्ह लेने पर ,
`(A_(1)B_(1))/(AB)=(+v_(0))/(-u_(0))`
`( :. ("प्रतिबिम्ब का आकार")/("वस्तु का आकार")=("लेन्स से प्रतिबिम्ब की दूरी")/("लेन्स से वस्तु की दूरी"))`
यदि नेत्रिका E से (इसके लिए आभासी वस्तु) `A_(1)B_(1)` की दूरी `u_(e)` हो तो उचित चिन्ह सहित
`EA_(1)=-u_(e)`
`:. ` समीकरण (5) में से मान रखने पर तथा D को ऋणात्मक लेने पर
`m=(+v_(0))/(u_(0))((-D)/(-u_(e)))` या `m=-[(v_(0))/(u_(0))((D)/(u_(e)))]` . . . .(6)

