प्रकाश का व्यतिकरण - प्रकाश का व्यतिकरण अध्यारोपण के सिद्धांत पर आधारित है " जब दो य दो से अधिक समान आवृत्ति की प्रकाश तरंगे जिनका आयाम समान या लगभग समान या लगभग समान हो एवं जिनके मध्य कलान्तर निश्चित हो , एक साथ किसी एक ही दिशा में माध्यम से गुजरती है तो उनके अध्यारोपण के कारण एक परिणामी तरंग की रचना होती है । परिणामी तरंग का आयाम किन्ही स्थानों पर अधिकतम एवं किन्ही स्थानों पर न्यूनतम होता है , फलस्वरूप उन बिन्दुओ पर परिणामी प्रकाश की तीव्रता भी अधिकतम या न्यूनतम होती है। " प्रकाश तरंगो की यह घटना व्यतिकरण कहलाती है । यंग का द्वि- स्लिट है। इस पर्दे के आगे कुछ की दूरी पर एक दूसरा पर्दा है जिसमे पार - पास दो स्लिट व है। ये दोनों स्लिट , पहले स्लिट की स्लिट की सीध में न होकर ऊपर नीचे है तथा से समान दूरियों पर है ।
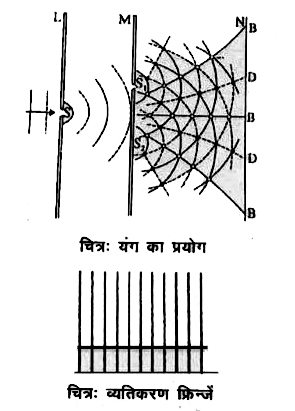
के आगे कुछ दूरी पर एक तीसरा पर्दा है। जब स्लिट पर एकवर्णी प्रकाश डालते है तो पर्दे पर समान चौड़ाई की दीप्त अतः अदीप्त पट्टियाँ एकान्तर कर्म में दिखाई देती है। चित्र में दीप्त पट्टी के स्थानों को से तथा अदीप्त पट्टी के स्थानों को से प्रदर्शित किया गया है। इन पत्तियों को फ्रिन्जे कहते है तथा फ्रिन्जो का यह समूह द्वी - स्लिट का व्यतिकरण - प्रतिरूप कहलाता है।
यंग के द्वि- स्लिट प्रयोग की सहायता से फ्रिन्ज चौड़ाई तथा प्रकाश की तरंगदैर्ध्य ज्ञात करना
चित्र में S एक संकीर्ण एकवर्णीय प्रकाश स्रोत्र है ,`S_(1)` तथा `S_(2)`इससे समान दूरी पर दो छिद्र है , जिनसे निकलने वाला प्रकाश कला सम्बद्ध होता है। अतः स्रोत्र कला सम्बद्ध होंगे। माना इनके मध्य दूरी d है । इन स्रोत्र से D दूरी पर स्थित पर्दे पर व्यतिकरण प्रतिरूप उत्पन्न उत्पन्न होता है।O. स्रोत्रों `S_(1)`व `S_(2)`का मध्य बिंदु पर तरंगो में पथान्तर शून्य होने के कारण प्रकाश की तीव्रता प्रतिरूप उत्पन्न होता है। स्रोत्रों व का मध्य बिंदु है। `S_(1)` व `S_(2)` के समान दूरी पर पर्दे पर स्थित बिंदु पर O तरंगो में पथान्तर शून्य होने के कारण प्रकाश की की अधिकतम होती है। माना बिंदु O से x दूरी पर स्थित बिंदु P पर प्रकाशीय तीव्रता की व्याख्या करनी है ।
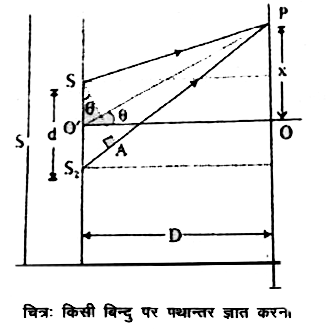
`S_(1)` व से P चलकर तक पहुँचने में तरंगिकाओं द्वारा तय की गई दूरियाँ क्रमशः `S_(1)P` व `S_(2)P` है। अतः इनके मध्य पथान्तर`Delta =S_(2)-S_(1)P` होगा। बिंदु `S_(1)` से `S_(2)`पर लम्ब `S_(1)A` है अतः `S_(1)P approx AP` होगा।
` :. ` पथान्तर =`S_(2)P - S_(2)P - S_(1)P -AP =S_(2)A`
चूँकि d का मान D की तुलना में बहुत कम होता है , अतः`S_(1)A` को O.P पर भी लम्ब मान सकते है ।
अतएव `angleS_(2)S_(1)= angleOOP.P = angle theta ` .
`triangle OO.P ` में `tan theta = (OP)/(OO.) = x/D` ,
`triangle S_(1)S_(2)A`में `sin theta = (S_(2)A)/(S_(2)S_(1))=(S_(2)A)/d " "....(2)`
अब यदि OP दूरी O.O की तुलना में अल्प हो तो का मान भी कम होगा अतः
`sin theta = tan theta cong theta` अतः समीकरण(1) व (2)से
`(S_(2)A)/d = c/D`
या पथान्तर `S_(2)A = Delta (xd)/D " "....(3)`
प्रदीप्त फ्रिज - यदि पथान्तर तरंगदैर्ध्य का पूर्ण गुणज अर्थात `nlambda` हो तो बिंदु P प्रदीप्त या चमकीला होगा यदि P पर n वीं प्रदीप्त फ्रिज बन रही हो एवं `x=x_(n)` हो तो समीकरण(3) से
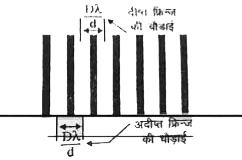
`(x_(n)d)/(D)=n lambda`
या `x_(n) = (nlambdaD)/d " "...(4)`
इसी तरह बिंदु O से`(n+1)` वीं प्रदीप्त फ्रिंज़`X_(n+l)` दूरी पर बने तो
`x_(n+1)= (n+1) (lambdaD)/d " " (6)`
अतः समीकरण(4) तथा(5) से किन्ही दो क्रमागत चमकीली के मध्य दूरी
`beta _(" ") = x_(n+1) - x_(n) = (lambdaD)/d " " ....(6) `
समीकरण(6) से स्पष्ट है की फ्रिंज़ चौड़ाई `(beta)` का मान n पर निर्भर नहीं करता है अतः सभी प्रदीप्त फ़्रिंजो की चौड़ाई समान होती है।


