आइंस्टीन का प्रकाश विद्युत समीकरण - आइन्स्टीन के अनुसार जब फोटोन किसी धातु की सतह पर गिरता है तो वह सारी ऊर्जा धातु के अंदर मुक्त इलेक्ट्रॉन को देता है । यह ऊर्जा जो इलेक्ट्रॉन प्राप्त करना है , यह दो कार्य करती है -
(i) इलेक्ट्रॉन को पदार्थ से बहार निकलने के लिए किए गए कार्य (कार्य फलन `W_(0)` ) के लिए ऊर्जा प्रदान करती हैं ।
इलेक्ट्रॉन को पदार्थ से बहार निकलने के पश्चात उसे गतिज प्रदान करती है `:.` आपतित फोटोन की ऊर्जा = धातु का कार्य फलन + इलेक्ट्रॉन की अधिकतम गतिज ऊर्जा
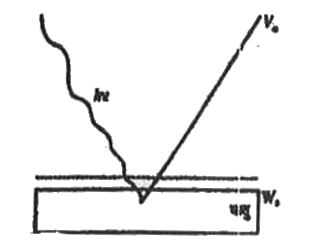
आपतित फोटोन की ऊर्जा `E = h upsilon` होती है ।
और कार्य फलन `W_(0) = h upsilon_(0)`
यहाँ पर `upsilon_(0)` धातु के लिए देहली आवृत्ति है ।
`upsilon_(0) = (C )/(lambda_(0))` ( `lambda_(0)` देहली तरंगदैर्ध्य है । )
इलेक्ट्रॉन की गतिज ऊर्जा
`K.E_("max") = (1)/(2) Mv_("max")^(2)`
यहाँ `V_("max")` उतसर्जित फोटो इलेक्ट्रॉन का अधिकतम वेग हैं (इलेक्ट्रॉन का वेग शून्य से `v_("max")` के बीच होता है । )
`E = W_(0) + KE_("max")`
समीकरण (1),(2),(3) तथा (4) से
`h upsilon = W_(0) + (1)/(2) Mv_("max")^(2)`
यहाँ `V_(m) = V_("max")` उतसर्जित इलेक्ट्रॉन का अधिकतम वेग है । समीकरण (6) से स्पष्ट है v के मान को कम करने पर उतसर्जित इलेक्ट्रॉन का वेग `v_("max")` कम होता है और `v_(0)` पर वेग शून्य हो जायेगा ।
समीकरण (6) से
`h upsilon = W_(0)`
`(h upsilon)/(lambda_(0)) = W_(0)`
उपर्युक्त समीकरण से स्पष्ट है की जब आपतित प्रकाश फोटोन की आवृत्ति `upsilon_(0)` से कम है तो इलेक्ट्रॉन का उतसर्जन संभव नहीं होगा
`:.` समीकरण (6) तथा समीकरण (7) से
`h upsilon = h upsilon_(0) + (1)/(2) mv_("max")^(2)`
`(1)/(2) mv_("max")^(2) = h upsilon - h upsilon_(0)`
`(1)/(2) mv_("max")^(2) = h (upsilon = upsilon_(0))`
अर्थात `K.E_("max") = h (upsilon - upsilon_(0))`
समीकरण आइंस्टीन का विद्युत समीकरण है ।
निरोधी विभव का व्यंजक
`(1)/(2) mv^(2) = eV_(0)`
आइंस्टीन का प्रकाश विद्युत समीकरण
`(1)/(2) mv^(2) = h upsilon - h upsilon_(0)`
समीकरण (1) व (2) से
`eV_(0) = h upsilon - h upsilon_(0)`
`V_(0) = (h (upsilon - upsilon_(0)))/(e)`
