Home
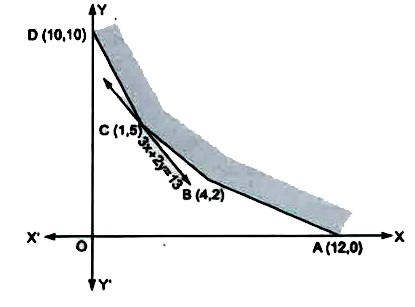
Class 12
MATHS
Determine the minimum value of Z = 3x + ...

Determine the minimum value of `Z = 3x + 2y` (if any), if the feasible region for an LPP is shown in figure:

A

Minimum value of Z = 11.

B

Minimum value of Z = 14.

C

Minimum value of Z = 12.

D

Minimum value of Z = 13.

Text Solution

Verified by Experts

The correct Answer is:
D
Promotional Banner

Topper's Solved these Questions

  • LINEAR PROGRAMMING

    MODERN PUBLICATION|Exercise FAQs|9 Videos

  • LINEAR PROGRAMMING

    MODERN PUBLICATION|Exercise (FAQ)|18 Videos

  • INVERSE - TRIGONOMETRIC FUNCTIONS

    MODERN PUBLICATION|Exercise CHAPTER TEST (2)|11 Videos

  • MATRICES

    MODERN PUBLICATION|Exercise CHAPTER TEST (3)|12 Videos

Similar Questions

Explore conceptually related problems

The maximum value of Z = 4x + 3y, if the feasible region for an LPP is shown in following figure, is

Determine the maximum value of Z=3x+4y, if the feasible reigon (shaded) for a LPP is shown in following figure

Find the maximum value of f(x,y)=3x+8y in following feasible region:

The maximum value of objective function Z = 3 x + y under given feasible region is

The maximum value of objective function z=2x+3y in the given feasible region is

The corner point method for bounded feasible region comprises of the following steps I. When the feasible region is bounded, M and m are the maximum and minimum values of Z. II. Find the feasible region of the linear programming problem and determine its corner points. Ill. Evaluate the objective function Z = ax + by at each corner point. Let M and m respectively be the largest and smallest values of these points. The correct order of these above steps is

Feasible region (shaded) for a LPP is shown in following figure. Maximise Z=5x+7y.

In a LPP, if the objective function Z=ax+by has the same maximum value of two corner points of the feasible region, then every point of the line segment joining these two points give the same ..value.

The feasible region for an LPP is shown in following figure. Find the minimum value of Z=11x+7y.

Consider the following statements I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist . II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region. Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region. IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite. Which of the following statements are true?