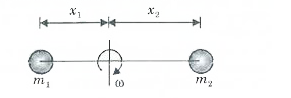
A
B
C
D
Text Solution
Verified by Experts
Topper's Solved these Questions
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
MODERN PUBLICATION|Exercise COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )|48 VideosSYSTEMS OF PARTICLES AND ROTATIONAL MOTION
MODERN PUBLICATION|Exercise COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )|35 VideosSYSTEMS OF PARTICLES AND ROTATIONAL MOTION
MODERN PUBLICATION|Exercise REVISION EXERCISES (Numerical Problems)|20 VideosPHYSICAL WORLD
MODERN PUBLICATION|Exercise Revision exercises (Long answer questions)|6 VideosTHERMAL PROPERTIES OF MATTER
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST|15 Videos
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MULTIPLE CHOICE QUESTIONS) (MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER) )
- Four identical rods each of mass m and length l are joined to form a r...
Text Solution
|
- A block of mass m is sliding down an inclined plane with uniform veloc...
Text Solution
|
- Two particles of masses m1 and m2 are joined y a light rigid rod of le...
Text Solution
|
- A solid sphere, disc and hollow sphere are placed at the top of an inc...
Text Solution
|
- A sphere a ring and a disc of same mass and radius are allowed to roll...
Text Solution
|
- A solid sphere, disc and hollow sphere of same masa and radius are pla...
Text Solution
|
- A large trolley is kept at rest on a frictionless horizontal surface. ...
Text Solution
|
- Let I(A) and I(B) be moments of inertia of a body about two axes A and...
Text Solution
|
- Two' blocks of masses m, and m, are connected to the two ends of a str...
Text Solution
|
- In which of the following cases it is certainly not possible for the d...
Text Solution
|
- The moment of inertia of a uniform rod of length 2l and mass m about a...
Text Solution
|
- Motion of the rigid body is observed from an inertial frame of referen...
Text Solution
|
- Motion of the rigid body is observed from an inertial frame of referen...
Text Solution
|
- If the radius of the earth contracts to half of its present value with...
Text Solution
|
- A particle is going around in a circular path with constant speed. Ang...
Text Solution
|
- The direction of the angular velocity vector is along
Text Solution
|
- The moments of inertia of two rotating bodies A and B are I(A) and I(B...
Text Solution
|
- A solid sphere rolls on a table without any slipping. What is the frac...
Text Solution
|
- There is a solid sphere of mass m. Moment of inertia about the axis pa...
Text Solution
|
- Calculate the moment of Inertia of a semicircular disc of mass M and r...
Text Solution
|